题目内容
已知平面上一个定点C(-1,0)和一条定直线L:x=-4,P为该平面上一动点,作PQ⊥L,垂足为Q,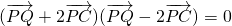 .
.
(1)求点P的轨迹方程;
(2)求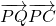 的取值范围.
的取值范围.
解:(1)由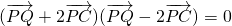 ,
,
得: 2分
2分
设P(x,y),得|x+4|2=4[(x+1)2+y2],
即 3x2+4y2=12,
∴点P的轨迹方程为 . 3分
. 3分
(2)设P(x,y), ,
,
 2分
2分
由x∈[-2,2],故有 3分.
3分.
分析:(1)先根据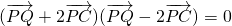 得到
得到 ,把点P的坐标代入整理即可求出点P的轨迹方程;
,把点P的坐标代入整理即可求出点P的轨迹方程;
(2)先根据向量的坐标运算求出 ,
, 的坐标,再代入
的坐标,再代入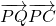 整理为关于x的函数,结合x的取值范围即可求出
整理为关于x的函数,结合x的取值范围即可求出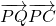 的取值范围.
的取值范围.
点评:本题主要考查平面向量数量积的运算.解决第一问的关键在于得到 .
.
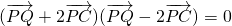 ,
,得:
 2分
2分设P(x,y),得|x+4|2=4[(x+1)2+y2],
即 3x2+4y2=12,
∴点P的轨迹方程为
 . 3分
. 3分(2)设P(x,y),
 ,
,
 2分
2分由x∈[-2,2],故有
 3分.
3分.分析:(1)先根据
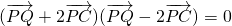 得到
得到 ,把点P的坐标代入整理即可求出点P的轨迹方程;
,把点P的坐标代入整理即可求出点P的轨迹方程;(2)先根据向量的坐标运算求出
 ,
, 的坐标,再代入
的坐标,再代入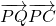 整理为关于x的函数,结合x的取值范围即可求出
整理为关于x的函数,结合x的取值范围即可求出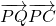 的取值范围.
的取值范围.点评:本题主要考查平面向量数量积的运算.解决第一问的关键在于得到
 .
. 
练习册系列答案
相关题目
 、
、 ,P为一个动点,且满足
,P为一个动点,且满足
 .
. .分别以A、B为切点作轨迹C的切线,设其交点为Q,证明
.分别以A、B为切点作轨迹C的切线,设其交点为Q,证明 为定值.
为定值.