题目内容
向量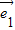 ,
,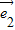 是单位向量,则
是单位向量,则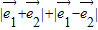 的取值范围是 .
的取值范围是 .
【答案】分析:设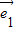 和
和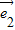 的夹角为θ,θ∈[0,π],由模长公式可化简式子为2cos
的夹角为θ,θ∈[0,π],由模长公式可化简式子为2cos +2sin
+2sin ,由三角函数的辅助角公式可求解其范围.
,由三角函数的辅助角公式可求解其范围.
解答:解:由题意可设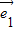 和
和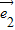 的夹角为θ,θ∈[0,π]
的夹角为θ,θ∈[0,π]
故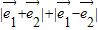 =
=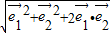 +
+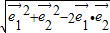
=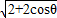 +
+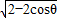 =
=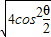 +
+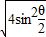
=2|cos |+2|sin
|+2|sin |,又θ∈[0,π],故
|,又θ∈[0,π],故 ∈[0,
∈[0,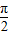 ],即cos
],即cos >0,sin
>0,sin ≥0,
≥0,
可得上式为:2cos +2sin
+2sin =2
=2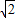 sin(
sin(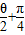 ),由与
),由与
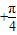 ∈[
∈[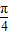 ,
,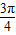 ],
],
故sin(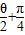 )∈[
)∈[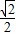 ,1],所以2
,1],所以2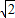 sin(
sin(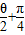 )∈[2,2
)∈[2,2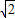 ],
],
故答案为: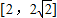
点评:本题考查向量的模长公式和三角函数的辅助角公式,属基础题.
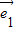 和
和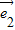 的夹角为θ,θ∈[0,π],由模长公式可化简式子为2cos
的夹角为θ,θ∈[0,π],由模长公式可化简式子为2cos +2sin
+2sin ,由三角函数的辅助角公式可求解其范围.
,由三角函数的辅助角公式可求解其范围.解答:解:由题意可设
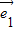 和
和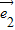 的夹角为θ,θ∈[0,π]
的夹角为θ,θ∈[0,π]故
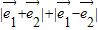 =
=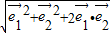 +
+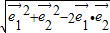
=
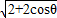 +
+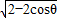 =
=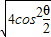 +
+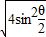
=2|cos
 |+2|sin
|+2|sin |,又θ∈[0,π],故
|,又θ∈[0,π],故 ∈[0,
∈[0,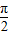 ],即cos
],即cos >0,sin
>0,sin ≥0,
≥0,可得上式为:2cos
 +2sin
+2sin =2
=2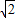 sin(
sin(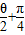 ),由与
),由与
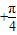 ∈[
∈[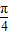 ,
,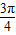 ],
],故sin(
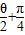 )∈[
)∈[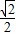 ,1],所以2
,1],所以2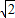 sin(
sin(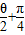 )∈[2,2
)∈[2,2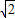 ],
],故答案为:
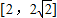
点评:本题考查向量的模长公式和三角函数的辅助角公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题正确的是( )
A、若
| ||||||||||||
B、若|
| ||||||||||||
C、若
| ||||||||||||
D、若
|
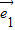 ,
,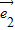 是单位向量,则
是单位向量,则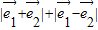 的取值范围是 .
的取值范围是 .