题目内容

直四棱柱ABCD-A1B1C1D1中，底面ABCD为菱形，且∠BAD=60°，A1A=AB，E为BB1延长线上的一点，D1E⊥面D1AC。

（Ⅰ）求二面角E-AC-D1的大小；
（Ⅱ）在D1E上是否存在一点P，使A1P∥面EAC？若存在，求D1P：PE的值；不存在，说明理由。

解：（Ⅰ）设AC与BD交于O，如图所示建立空间直角坐标系，
设AB=2，
则
设
则

∴
∴2-2h=0，∴h=1，即，
∴，
设平面EAC的法向量为，
则由，得，
令z=-1，
∴，

∴，
∴。
（Ⅱ）设
得
∴，
，
∴，
∴，
∴，
∴存在点P使A1P∥面EAC，此时D1P：PE=2：3。
练习册系列答案
相关题目
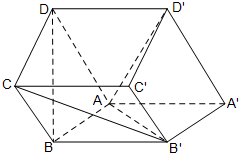精英家教网如图，在直四棱柱ABCD-A′B′C′D′中，底面ABCD为梯形，BC∥AD，AA′=AB=
2
，AD=2BC=2，直线AD与面ABB'A'所成角为45°．
（Ⅰ）求证：DB⊥面ABB'A'；
（Ⅱ）求证：AD'⊥B'C；
（Ⅲ）求二面角D-AB'-B的正切值．
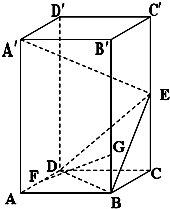精英家教网已知直四棱柱ABCD-A′B′C′D′，四边形ABCD为正方形，AA′=2AB=2，E为棱CC′的中点．
（Ⅰ）求证：A′E⊥平面BDE；
（Ⅱ）设F为AD中点，G为棱BB′上一点，且BG=
14
BB′，求证：FG∥平面BDE；
（Ⅲ）在（Ⅱ）的条件下求二面角G-DE-B的余弦值．
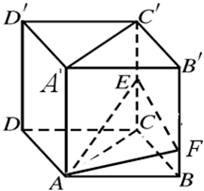已知直四棱柱ABCD-A′B′C′D′的底面是菱形，∠ABC=60°，E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2．
（1）求证：平面AEF⊥平面AA′C′C；
（2）求截面AEF与底面ABCD的夹角的大小．
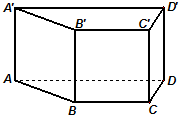在高为1的直四棱柱ABCD-A'B'C'D'中，底面ABCD是等腰梯形，AB=BC=CD=1，AD=2． 
（1）求异面直线BC'与CD'所成的角；
（2）求被截面ACD'所截的两部分几何体的体积比．
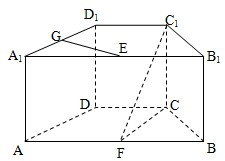（2009•崇明县一模）如图，在直四棱柱ABCD-A'B'C'D'中，底面ABCD为等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E、F、G分别是棱A1B1、AB、A1D1的中点．
（1）证明：直线GE⊥平面FCC1；
（2）求二面角B-FC1-C的大小．