题目内容
椭圆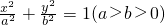 顶点A(a,0),B(0,b),若右焦点F到直线AB的距离等于
顶点A(a,0),B(0,b),若右焦点F到直线AB的距离等于 ,则椭圆的离心率e=
,则椭圆的离心率e=
- A.

- B.

- C.

- D.

B
分析:由题意可得直线AB的方程为 ,由F(c,0)到直线AB的距离d=
,由F(c,0)到直线AB的距离d= =
= ,|AF|=a-c,结合已知可得a,b之间关系,结合a2-c2=b2及
,|AF|=a-c,结合已知可得a,b之间关系,结合a2-c2=b2及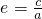 可求
可求
解答: 解:由题意可得直线AB的方程为
解:由题意可得直线AB的方程为 即bx+ay-ab=0,F(c,0)
即bx+ay-ab=0,F(c,0)
∴F(c,0)到直线AB的距离d= =
= ,|AF|=a-c
,|AF|=a-c
则
∴a2=3b2
∴a2=3a2-3c2
即3c2=2a2
∴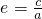 =
=
故选B
点评:本题主要考查了椭圆的性质的应用,直线方程的截距式及点到直线的距离公式的应用,属于中档试题
分析:由题意可得直线AB的方程为
 ,由F(c,0)到直线AB的距离d=
,由F(c,0)到直线AB的距离d= =
= ,|AF|=a-c,结合已知可得a,b之间关系,结合a2-c2=b2及
,|AF|=a-c,结合已知可得a,b之间关系,结合a2-c2=b2及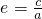 可求
可求解答:
 解:由题意可得直线AB的方程为
解:由题意可得直线AB的方程为 即bx+ay-ab=0,F(c,0)
即bx+ay-ab=0,F(c,0)∴F(c,0)到直线AB的距离d=
 =
= ,|AF|=a-c
,|AF|=a-c则

∴a2=3b2
∴a2=3a2-3c2
即3c2=2a2
∴
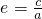 =
=
故选B
点评:本题主要考查了椭圆的性质的应用,直线方程的截距式及点到直线的距离公式的应用,属于中档试题

练习册系列答案
相关题目
 ,过椭圆左顶点A(-a,0)的直线L与椭圆交于Q,与y轴交于R,过原点与L平行的直线与椭圆交于P,求证:AQ,
,过椭圆左顶点A(-a,0)的直线L与椭圆交于Q,与y轴交于R,过原点与L平行的直线与椭圆交于P,求证:AQ, ,AR成等比数列.
,AR成等比数列. ,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2.
,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2. .
.