题目内容
函数f(x)=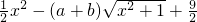 ,g(x)=ax2-b(a、b、x∈R)),A={x|
,g(x)=ax2-b(a、b、x∈R)),A={x|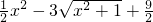 ≤0}
≤0}
(Ⅰ)求集合A;
(Ⅱ)如果b=0,对任意x∈A时,f(x)≥0恒成立,求实数a的范围;
(Ⅲ)如果b>0,当“f(x)≥0对任意x∈A恒成立”与“g(x)≤0在x∈A内必有解”同时成立时,求3a+b的最大值.
解:(Ⅰ)令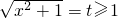 ,则x2=t2-1,
,则x2=t2-1,
f(x)≤0即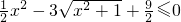 即t2-6t+8≤0,
即t2-6t+8≤0,
∴2≤t≤4,所以 ,所以x∈[-
,所以x∈[- ,-
,- ]∪[
]∪[ ,
, ],
],
即A=[- ,-
,- ]∪[
]∪[ ,
, ],…
],…
(Ⅱ)f(x)≥0恒成立也就是f(x)=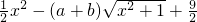 ≥0恒成立,
≥0恒成立,
∵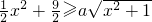 ,即
,即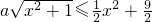 ,
,
∵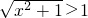 ,
,
a≤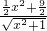 =
=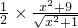 =
=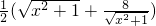 恒成立,
恒成立,
因为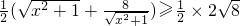 =2
=2 ,所以a
,所以a .
.
…
(Ⅲ)对任意x∈A,f(x)≥0恒成立,a+b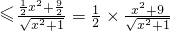
得a+b ,
,
由g(x)=ax2-b≤0有解,ax2-b≤0有解,即a≤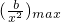 ,
,
∵b>0,∴a≤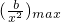 =
= ,≥3a. …
,≥3a. …
∴a,b满足条件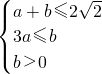 所表示的区域,设3a+b=t,b=-3a+t,
所表示的区域,设3a+b=t,b=-3a+t,
根据可行域求出当a= ,b=
,b= 时取得.
时取得.
所以3a+b的最大值为3 . …
. …
分析:(Ⅰ)利用换元法直接求解不等式的解集,即可得到集合A;
(Ⅱ)通过b=0,对任意x∈A时,f(x)≥0恒成立,转化为函数的最值问题,通过基本不等式,即可实数a的范围;
(Ⅲ)利用b>0,当“f(x)≥0对任意x∈A恒成立”与“g(x)≤0在x∈A内必有解”同时成立,转化为线性规划问题,然后求3a+b的值.
点评:本题考查不等式的解法,函数的最值以及线性规划基本不等式的应用,考查转化思想与计算能力.
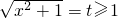 ,则x2=t2-1,
,则x2=t2-1,f(x)≤0即
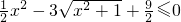 即t2-6t+8≤0,
即t2-6t+8≤0,∴2≤t≤4,所以
 ,所以x∈[-
,所以x∈[- ,-
,- ]∪[
]∪[ ,
, ],
],即A=[-
 ,-
,- ]∪[
]∪[ ,
, ],…
],…(Ⅱ)f(x)≥0恒成立也就是f(x)=
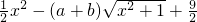 ≥0恒成立,
≥0恒成立,∵
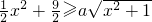 ,即
,即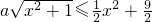 ,
,∵
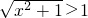 ,
,a≤
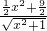 =
=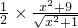 =
=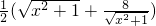 恒成立,
恒成立,因为
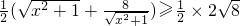 =2
=2 ,所以a
,所以a .
.…
(Ⅲ)对任意x∈A,f(x)≥0恒成立,a+b
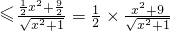
得a+b
 ,
,由g(x)=ax2-b≤0有解,ax2-b≤0有解,即a≤
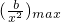 ,
,∵b>0,∴a≤
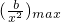 =
= ,≥3a. …
,≥3a. …∴a,b满足条件
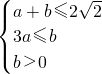 所表示的区域,设3a+b=t,b=-3a+t,
所表示的区域,设3a+b=t,b=-3a+t,根据可行域求出当a=
 ,b=
,b= 时取得.
时取得.所以3a+b的最大值为3
 . …
. …分析:(Ⅰ)利用换元法直接求解不等式的解集,即可得到集合A;
(Ⅱ)通过b=0,对任意x∈A时,f(x)≥0恒成立,转化为函数的最值问题,通过基本不等式,即可实数a的范围;
(Ⅲ)利用b>0,当“f(x)≥0对任意x∈A恒成立”与“g(x)≤0在x∈A内必有解”同时成立,转化为线性规划问题,然后求3a+b的值.
点评:本题考查不等式的解法,函数的最值以及线性规划基本不等式的应用,考查转化思想与计算能力.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目



