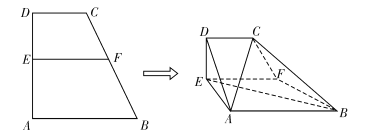
[题目]将边长为的正方形绕旋转一周形成圆柱.如图. 长为. 长为.其中与在平面的同侧. (1)求三棱锥的体积,(2)求异面直线与所成的角的大小. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】将边长为的正方形（及其内部）绕旋转一周形成圆柱，如图，长为，长为，其中与在平面的同侧.

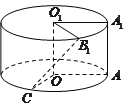
(1)求三棱锥的体积；

(2)求异面直线与所成的角的大小.

【答案】(1) (2) .

【解析】试题分析：（1）由题意可知，圆柱的高，底面半径，，再由三角形面积公式计算后即得.

（2）设过点的母线与下底面交于点，根据，知或其补角为直线与所成的角，再结合题设条件确定，．得出即可．

试题解析：（1）由题意可知，圆柱的高，底面半径．

由的长为，可知．

，

．

（2）设过点的母线与下底面交于点，则，

所以或其补角为直线与所成的角．

由长为，可知，

又，所以，

从而为等边三角形，得．

因为平面，所以．

在中，因为，，，所以，

从而直线与所成的角的大小为．

练习册系列答案

【题目】设直线y=t与曲线C：y=x（x﹣3）2的三个交点分别为A（a，t），B（b，t），C（c，t），且a＜b＜c．现给出如下结论：

①abc的取值范围是（0，4）；

②a2+b2+c2为定值；③a+b+c=6

其中正确结论的为_______

【题目】已知椭圆的离心率为，且椭圆过点，直线过椭圆的右焦点且与椭圆交于两点.

(Ⅰ)求椭圆的标准方程；

(Ⅱ)已知点，求证：若圆与直线相切，则圆与直线也相切.

【题目】已知直角梯形中，，，，、分别是边、上的点，且，沿将折起并连接成如图的多面体，折后．

（Ⅰ）求证：；

（Ⅱ）若折后直线与平面所成角的正弦值是，求证：平面平面．

【题目】已知函数y＝f(x)和y＝g(x)在[－2,2]上的图象如图所示．给出下列四个命题：

①方程f[g(x)]＝0有且仅有6个根；②方程g[f(x)]＝0有且仅有3个根；

③方程f[f(x)]＝0有且仅有7个根；④方程g[g(x)]＝0有且仅有4个根．

其中正确命题的序号为________.

【题目】已知函数满足，其中且.

（1）对于函数，当时，，求实数的集合；

（2）时，的值恒为负数，求的取值范围.

【题目】已知函数.

（1）求函数的单调增区间；

（2）设，若，对任意成立，求实数的取值范围.

【题目】北京时间3月15日下午，谷歌围棋人工智能与韩国棋手李世石进行最后一轮较量，获得本场比赛胜利，最终人机大战总比分定格.人机大战也引发全民对围棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

（Ⅰ）根据已知条件完成下面的列联表，并据此资料你是否有的把握认为“围棋迷”与性别有关？

	非围棋迷	围棋迷	合计
男
女		10	55
合计

（Ⅱ）将上述调查所得到的频率视为概率，现在从该地区大量学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记被抽取的3名淡定生中的“围棋迷”人数为。若每次抽取的结果是相互独立的，求的分布列，期望和方差.

附：，其中.

	0.05	0.01
	3.841	6.635

试题分类