题目内容

7．sin65°cos20°-cos65°sin20°=（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．$\frac{\sqrt{2}}{2}$D．-$\frac{\sqrt{2}}{2}$

分析 利用两角差的正弦公式，求得要求式子的值．

解答 解：sin65°cos20°-cos65°sin20°=sin（65°-20°）=sin45°=$\frac{\sqrt{2}}{2}$，
故选：C．

点评 本题主要考查两角差的正弦公式的应用，属于基础题．

练习册系列答案
相关题目
1．设f（x）=|lgx|，a，b满足f（a）=f（b）=2f（$\frac{a+b}{2}$）的实数，其中0＜a＜b，则4b-b2的取值范围是（　　）
A．（1，2）B．（2，3）C．（3，4）D．（4，5）
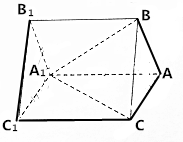2．在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2，∠BAA1=∠CAA1=60°，异面直线A1C1与BC成角为45°．
（1）求证：AA1⊥BC；
（2）求二面角B-AA1-C的余弦值；
（3）求直线A1B于平面A1AC所成角的正弦值．
15．已知正项数列{an}的前n项和为Sn，满足：an2=2Sn-an（n∈N+）
（1）证明：数列{an}为等差数列，并求数列{an}的通项公式；
（2）设bn=3n+（-1）n-1λ•2an，是否存在整数λ（λ≠0），使bn+1＞bn对一切n∈N+恒成立？若存在，求出λ；若不存在，说明理由．
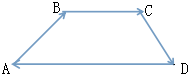2．如图所示的四边形ABCD，已知$\overrightarrow{AB}$=（6，1），$\overrightarrow{BC}$=（x，y），$\overrightarrow{CD}$=（-2，-3）
（1）若$\overrightarrow{BC}∥\overrightarrow{DA}$且-2≤x＜1，求函数y=f（x）的值域；
（2）若$\overrightarrow{BC}∥\overrightarrow{DA}$且$\overrightarrow{AC}⊥\overrightarrow{BD}$，求x，y的值及四边形ABCD的面积．
12．已知命题p：?x∈R，x-2＞0，命题q：?x∈R，$\sqrt{x}$＞x，则下列说法中正确的是④．
①命题p∨q是假命题          
②命题p∧q是真命题
③命题p∨（￢q）是假命题      
④命题p∧（￢q）是真命题．
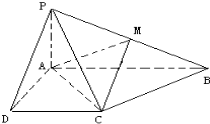19．已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=$\frac{1}{2}$AB=1，M是PB的中点．
（1）证明：CD⊥面PAD；
（2）求直线AC与PB所成的角；
（3）求点P到平面MAC的距离．
16．判断下列对应哪些是由A到B的映射？为什么？
（1）A=R，B={y|y＞0}，f：x→y=1+$\frac{1}{|x|}$
（2）A=R，B={y|y≥0}，f：x→y=x2
（3）A={x|x≥3}，B={y|y≥0}，f：x→y=$\sqrt{x}$．
17．已知下列随机变量：
①10件产品中有2件次品，从中任选3件，取到次品的件数X；
②一位射击手对目标进行射击，击中目标得1分，未击中目标得0分，用X表示该射击手在一次射击中的得分；
③刘翔在一次110米跨栏比赛中的成绩X；
④在体育彩票的抽奖中，一次摇号产生的号码数X．
其中X是离散型随机变量的是（　　）
A．①②③B．②③④C．①②④D．③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网