题目内容
如图,在四棱锥 中,
中, 底面ABCD,底面ABCD是直角梯形,
底面ABCD,底面ABCD是直角梯形, ,
, ,
, ,
, 是
是 的中点
的中点
(1)求证:平面 平面
平面 ;
;
(2)若二面角 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面 所成角的正弦值
所成角的正弦值


试题解析:(1)证明: 平面ABCD,
平面ABCD, 平面ABCD,
平面ABCD, ,
,
 ,
, ,
,
 ,
, 又
又 ,
, 平面
平面 ,
,
∵ 平面EAC,
平面EAC, 平面
平面 平面
平面 6分
6分
(2)以 为原点,建立空间直角坐标系如图所示,
为原点,建立空间直角坐标系如图所示,


则C(0,0,0), (1,1,0),
(1,1,0), (1,-1,0)
(1,-1,0)
设 (0,0,
(0,0, )(
)( ),则
),则 (
( ,
, ,
, ),
),
 ,
, ,
, ,
,
取 =(1,-1,0) 8分
=(1,-1,0) 8分
则 ,
,
 为面
为面 的法向量
的法向量
设 为面
为面 的法向量,则
的法向量,则 ,
,
即 ,取
,取 ,
, ,
, ,
,
则 ,
,
依题意, ,则
,则 10分
10分
于是
设直线 与平面
与平面 所成角为
所成角为 ,则
,则 ,
,
即直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 12分
12分
考点:1、平面与平面垂直的判定;2平面与平面所成角的正弦值.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知x与y 之间的一组数据:则y与x的线性回归方程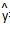 =bx+a必过点 ( )
=bx+a必过点 ( )
A.(1,2) B.(1.5,0) C.(2,2) D.(1.5,4)
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
 满足
满足 ,且在
,且在 上的解析式为
上的解析式为 ,则
,则
 的函数
的函数 对任意的
对任意的 都有
都有 ,且其导函数
,且其导函数 满足:
满足: ,则当
,则当 时,下列成立的是 ( )
时,下列成立的是 ( ) B.
B.
 D.
D.
 的一条渐近线与圆
的一条渐近线与圆
 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) C 3 D.4
C 3 D.4 满足约束条件
满足约束条件 若
若 的最大值为11,则实数
的最大值为11,则实数 ,
, ,则 ( )
,则 ( ) B.
B. C.
C. D.
D.

 B.2 C.-1 D.-
B.2 C.-1 D.- 和
和 满足:
满足: ,
, ,
, ,
, 是等差数列;
是等差数列; 令
令 ,求证:
,求证: .
.