Question

【题目】如图1，在四边形中，，，，.把沿着翻折至的位置，构成三棱锥如图2.

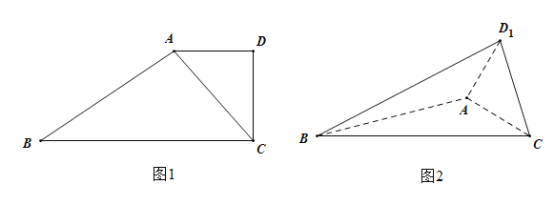
（1）当时，证明：；

（2）当三棱锥的体积最大时，求点到平面的距离.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）由题易得，再证，可得平面，最后得出即可；

（2）设到面的距离，要使取到最大值，需且仅需取到最大值，再取的中点，连结，分析可得当且仅当平面平面时，取得最大值，，设到平面的距离为，利用等体积法计算出即可.

（1）因为，，，，

依题意得，，即，，

因为，所以，故，即，

又因为，，所以平面，；

（2）因为，，，，所以的面积为，

设到面的距离，则三棱锥的体积为，

故要使取到最大值，需且仅需取到最大值，

取的中点，连结，如下图，依题意知，，

所以，，且，

因为平面平面，，平面，

所以当平面平面时，平面，故，

故当且仅当平面平面时，取得最大值，

此时，

设到平面的距离为，可得，

故，解得，故到平面的距离为.