题目内容
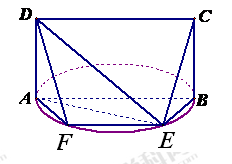
如图,四边形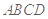 为矩形,
为矩形, 平面
平面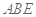 ,
,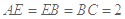 ,
,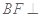 平面
平面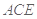 于点
于点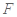 ,且点
,且点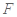 在
在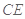 上.
上.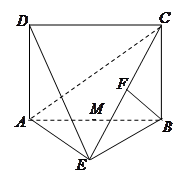
(1)求证: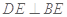 ;
;
(2)求四棱锥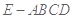 的体积;
的体积;
(3)设点 在线段
在线段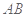 上,且
上,且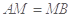 ,试在线段
,试在线段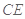 上确定一点
上确定一点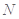 ,使得
,使得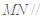 平面
平面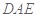 .
.
(1)证明略;(2) ;(3)存在点N即为点F使得
;(3)存在点N即为点F使得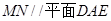 .
.
解析试题分析:(1)先由 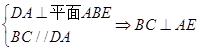 ,又
,又 ,由线面垂直的判定定理由
,由线面垂直的判定定理由 ,根据面面垂直的性质定理有
,根据面面垂直的性质定理有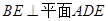 ,可证线线垂直
,可证线线垂直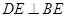 ;
;
(2) 由(1)可知该几何体是一个四棱锥,作 ,因为
,因为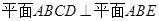 ,所以
,所以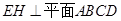 ,所以
,所以 ;
;
(3) 由已知有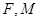 分别为
分别为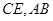 的中点,只需要取
的中点,只需要取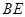 的中点
的中点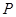 ,由
,由
则点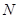 就是点
就是点 .
.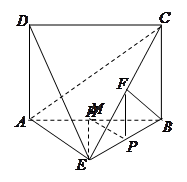
试题解析:(1)因为 平面
平面 ,
, ∥
∥
所以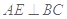 ,
,
因为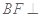 平面
平面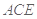 于点
于点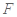 ,
,
因为 ,所以
,所以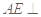 面
面 ,
,
则
因为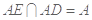 ,所以
,所以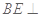 面
面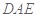 ,
,
则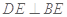
(2)作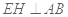 ,因为面
,因为面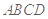
 平面
平面 ,所以
,所以 面
面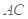
因为 ,
,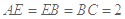 ,所以
,所以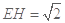
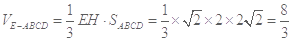
(3)因为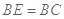 ,
,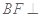 平面
平面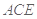 于点
于点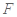 ,所以
,所以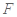 是
是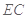 的中点
的中点
设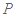 是
是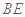 的中点,连接
的中点,连接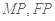
所以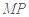 ∥
∥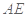
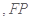 ∥
∥
因为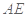

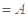 ,所以
,所以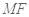 ∥面
∥面 ,则点
,则点 就是点
就是点
考点:1、线面平行的性质;2、线面垂直的性质定理;3、线面垂直的判定定理;4、面面垂直的性质定理;5、四棱锥的体积公式;6、面面平行的判定地理;7、探究存在性问题.

练习册系列答案
相关题目
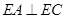
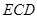 与半圆弧的另一个交点为
与半圆弧的另一个交点为
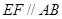
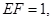 求三棱锥
求三棱锥 的体积
的体积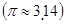
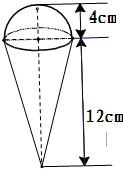
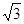 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
 中,侧棱长均为
中,侧棱长均为 ,底边
,底边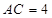 ,
, ,
, ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
 的平面角.
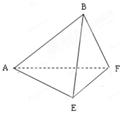
的平面角. 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).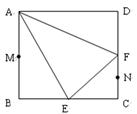
 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;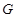 是线段
是线段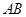 上一点,且
上一点,且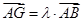 ,问是否存在点
,问是否存在点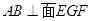 ,若存在,求出
,若存在,求出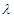 的值;若不存在,请说明理由;
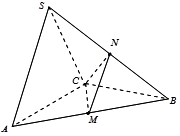
的值;若不存在,请说明理由;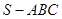 中,
中, 是边长为
是边长为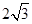 的正三角形,平面
的正三角形,平面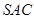 ⊥平面
⊥平面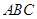 ,
,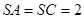 ,
,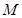 、
、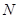 分别为
分别为 、
、 的中点.
的中点.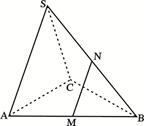
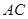 ⊥
⊥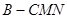 的体积.
的体积.  中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 为
为 的中点,已知
的中点,已知 ,
,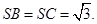
 ;
;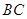 上求一点
上求一点 ,使
,使 平面
平面 ;
; 的体积.
的体积.