题目内容
已知命题“p:双曲线C的离心率为
”,命题“q:双曲线C为等轴双曲线”.则p是q的( )
| 2 |
分析:双曲线C的离心率为
,求出双曲线方程判断是不是等轴双曲线,以及双曲线C为等轴双曲线求出离心率,即可判断充要条件.
| 2 |
解答:解:双曲线C的离心率为
,所以c=
a,并且a=b,所以双曲线为等轴双曲线,
对于命题q,双曲线C为等轴双曲线,所以a=b,c=
a,所以e=
.
所以命题“p:双曲线C的离心率为
”,命题“q:双曲线C为等轴双曲线”.
则p是q的充要条件.
故选C.
| 2 |
| 2 |
对于命题q,双曲线C为等轴双曲线,所以a=b,c=
| 2 |
| 2 |
所以命题“p:双曲线C的离心率为
| 2 |
则p是q的充要条件.
故选C.
点评:本题考查双曲线的离心率与等轴双曲线的关系,充要条件的应用.

练习册系列答案
相关题目
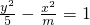 的离心率
的离心率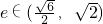 ,命题q:方程
,命题q:方程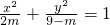 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.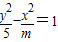 的离心率
的离心率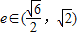 ,命题q:方程
,命题q:方程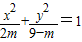 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.