题目内容
已知命题p:双曲线
-
=1的离心率e∈(
,
),命题q:方程
+
=1表示焦点在y轴上的椭圆.
(1)若命题p是真命题,求实数m的取值范围;
(2)若命题“p∧q”是真命题,求实数m的取值范围.
| y2 |
| 5 |
| x2 |
| m |
| ||
| 2 |
| 2 |
| x2 |
| 2m |
| y2 |
| 9-m |
(1)若命题p是真命题,求实数m的取值范围;
(2)若命题“p∧q”是真命题,求实数m的取值范围.
分析:(1)根据双曲线标准的方程与双曲线的有关性质可得m>0,且e2=1+
=1+
∈(
,2),进而求出m的范围.
(2)根据题意分别求出命题p、q为真时m的范围,再结合命题“p∧q”是真命题,则p、q都是真命题,进而求出m的范围.
| b2 |
| a2 |
| m |
| 5 |
| 3 |
| 2 |
(2)根据题意分别求出命题p、q为真时m的范围,再结合命题“p∧q”是真命题,则p、q都是真命题,进而求出m的范围.
解答:解:(1)p真,则有m>0,且e2=1+
=1+
∈(
,2),
所以
<m<5.--------(5分)
(2)q真,则有9-m>2m>0,
所以0<m<3.-----------------(9分)
若命题“p∧q”是真命题,则p、q都是真命题.
故所求范围为
<m<3-----------------(12分)
| b2 |
| a2 |
| m |
| 5 |
| 3 |
| 2 |
所以
| 5 |
| 2 |
(2)q真,则有9-m>2m>0,
所以0<m<3.-----------------(9分)
若命题“p∧q”是真命题,则p、q都是真命题.
故所求范围为
| 5 |
| 2 |
点评:解决此类问题的关键是熟练掌握命题真假的判定方法,由复合命题的真假判断出简单命题的真假结合椭圆与双曲线的有关知识进行判断解题即可.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
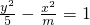 的离心率
的离心率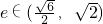 ,命题q:方程
,命题q:方程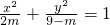 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.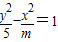 的离心率
的离心率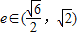 ,命题q:方程
,命题q:方程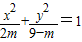 表示焦点在y轴上的椭圆.
表示焦点在y轴上的椭圆.