题目内容
8. 如图,当抛物线形拱桥的拱顶距水面2米时,测得水面宽4米.若水面下降0.5米,则水面宽$2\sqrt{5}$米.
如图,当抛物线形拱桥的拱顶距水面2米时,测得水面宽4米.若水面下降0.5米,则水面宽$2\sqrt{5}$米.
分析 可建立平面直角坐标系,设抛物线的方程为x2=2py,从而由题意知点(2,-2)在抛物线上,带入抛物线方程便可求出p=-1,这便得出抛物线方程为x2=-2y.而根据题意知点(x0,-2.5)在抛物线上,从而可以求出x0,从而水面宽度便为2|x0|,即得出水面宽度.
解答 解:建立如图所示平面直角坐标系:
设抛物线方程为x2=2py;
根据题意知,A(2,-2)在抛物线上;
∴4=2p•(-2);
∴p=-1;
∴x2=-2y;
设B(x0,-2.5)在抛物线上,则:${{x}_{0}}^{2}=-2•(-2.5)$;
∴${x}_{0}=±\sqrt{5}$;
∴水面下降0.5米,则水面宽为$2\sqrt{5}$.
故答案为:$2\sqrt{5}$.
点评 考查通过建立平面直角坐标系,根据曲线上点的坐标求出曲线方程,利用曲线方程解决几何问题的方法,以及抛物线的标准方程,数形结合解题的方法.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
18.设P点为角α的终边与单位圆O的交点,且sinα=MP,cosα=OM,则下列命题成立的是( )
| A. | 总有MP+OM>1 | B. | 总有MP+OM=1 | ||
| C. | 存在角α,使MP+OM=1 | D. | 不存在角α,使MP+OM<0 |
20.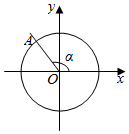 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A.若点A的纵坐标是$\frac{4}{5}$,那么sinα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
17.从点P(-2,1)向圆x2+y2-2x-2my+m2=0作切线,当切线长最短时,m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
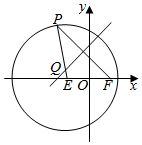 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.