题目内容
过点P(2,1)与直线l:y=3x-4垂直的直线方程为 .
【答案】分析:与直线l:y=3x-4垂直的直线的斜率k=- ,由此能求出过点P(2,1)且与直线l:y=3x-4垂直的直线方程.
,由此能求出过点P(2,1)且与直线l:y=3x-4垂直的直线方程.
解答:解:∵与直线l:y=3x-4垂直的直线的斜率k=- ,
,
∴过点P(2,1)与直线l:y=3x-4垂直的直线方程为:
y-1=- (x-2),整理,得x+3y-5=0.
(x-2),整理,得x+3y-5=0.
故答案为:x+3y-5=0.
点评:本题考查直线方程的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.
 ,由此能求出过点P(2,1)且与直线l:y=3x-4垂直的直线方程.
,由此能求出过点P(2,1)且与直线l:y=3x-4垂直的直线方程.解答:解:∵与直线l:y=3x-4垂直的直线的斜率k=-
 ,
,∴过点P(2,1)与直线l:y=3x-4垂直的直线方程为:
y-1=-
 (x-2),整理,得x+3y-5=0.
(x-2),整理,得x+3y-5=0.故答案为:x+3y-5=0.
点评:本题考查直线方程的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 椭圆E:
椭圆E: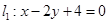 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
.