题目内容
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数,且
的导函数,且![]() .
.
(1)求![]() 的值,并证明
的值,并证明![]() 在
在![]() 处取得极值;
处取得极值;
(2)证明:![]() 在区间
在区间![]() 有唯一零点.
有唯一零点.
【答案】(1)![]() ,证明见解析(2)证明见解析
,证明见解析(2)证明见解析
【解析】
(1)求出导函数,根据![]() 求出
求出![]() 的值,再通过计算导函数的正负情况说明函数的单调性,计算出极值点.
的值,再通过计算导函数的正负情况说明函数的单调性,计算出极值点.
(2)根据![]() ,
,![]() 由零点存在性定理可知函数
由零点存在性定理可知函数![]() 在区间
在区间![]() 有零点,再证明零点的唯一性即可.
有零点,再证明零点的唯一性即可.
解:(1)![]() ,令
,令![]() ,得
,得![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 是区间
是区间![]() 上的增函数.
上的增函数.
当![]() 时,令
时,令![]() ,则
,则![]() ,在区间
,在区间![]() 上,
上,![]() ,故
,故![]() 是
是![]() 上的减函数,∴
上的减函数,∴![]() ,即在区间
,即在区间![]() 上,
上,![]() ,因此
,因此![]() 是区间
是区间![]() 上的减函数.综上所述,
上的减函数.综上所述,![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
(2)由(1)![]() ,∵
,∵![]() (当且仅当
(当且仅当![]() 时,
时,![]() .)
.)
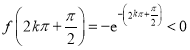 ,∴
,∴![]() 在区间
在区间![]() 至少有一个零点.
至少有一个零点.
以下讨论![]() 在区间
在区间![]() 上函数值的变化情况:
上函数值的变化情况:
由(1)![]() ,令
,令![]() ,则
,则![]() ,
,
令![]() ,在
,在![]() 上,解得
上,解得![]() ,
,![]() .
.
①当![]() 时,在区间
时,在区间![]() ,
,![]() ,
,![]() 递减,
递减,![]() ;在
;在![]() ,
,![]() ,
,![]()
递增,![]() .故存在唯一实数
.故存在唯一实数![]() ,使
,使![]() ,即
,即![]() .在
.在![]()
上,![]() ,
,![]() 递减,
递减,![]() ;在
;在![]() 上,
上,![]() ,
,![]() 递增,而
递增,而![]() ,故在
,故在![]() 上,
上,![]() ,当且仅当
,当且仅当![]() 时,
时,![]() .故
.故![]() 在
在![]() 上有唯一零点.
上有唯一零点.
②对任意正整数![]() ,在区间
,在区间![]() ,
,![]() ,
,![]() 递减,
递减,![]() ,
,
在区间![]() ,
,![]() ,
,![]() 递增,
递增,![]() ,故存在唯一实数
,故存在唯一实数![]() ,使
,使![]() ,即
,即![]() ,在
,在![]() 上,因
上,因![]() ,故
,故![]() ,
,![]() 递减,在
递减,在![]() 上,因
上,因![]() ,故
,故![]() ,
,![]() 递增,
递增,![]() ,
,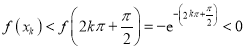 ,∴
,∴![]() ,
,
∴![]() 在区间
在区间![]() 即
即![]() 有唯一零点.
有唯一零点.
综上,![]() 在区间
在区间![]() 有唯一零点.
有唯一零点.

【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()