题目内容
函数y=
sinxcosx-sin2x的最小正周期为 ,最大值为 .
| 3 |
分析:先利用二倍角公式和两角和的正弦公式将函数化简为y=Asin(ωx+φ)型函数,再利用周期计算公式计算其最小正周期,最后利用正弦函数的图象和性质求函数的最大值即可
解答:解:y=
sinxcosx-sin2x=
sin2x-
(1-cos2x)=
sin2x+
cos2x-
=sin(2x+
)-
∴函数的最小正周期为
=π,
当sin(2x+
)=1时,函数取得最大值1-
=
故答案为 π,
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∴函数的最小正周期为
| 2π |
| 2 |
当sin(2x+
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为 π,
| 1 |
| 2 |
点评:本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,三角变换公式在化简求值中的应用,属基础题

练习册系列答案
相关题目
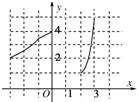 13、函数y=f(x)的图象如图所示.那么,f(x)的定义域是
13、函数y=f(x)的图象如图所示.那么,f(x)的定义域是