题目内容
11.已知点M(6,-8),点P(x,y)满足不等式(x-3)2+(y+2)2≤25,则$\overrightarrow{OM}•\overrightarrow{OP}$的取值范围为( )| A. | [-16,84] | B. | [-50,50] | C. | [-16,16] | D. | [-16,50] |
分析 P在圆内运动,$\overrightarrow{OM}•\overrightarrow{OP}$=6x-8y,将问题转化为线性规划解决.
解答 解:由题意可知点P的可行域在圆(x-3)2+(y+2)2=25内部(含边界).
作出可行域如图: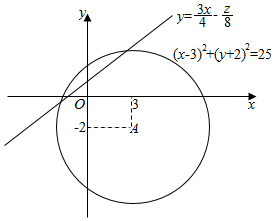
令z=$\overrightarrow{OM}•\overrightarrow{OP}$=6x-8y,则y=$\frac{3x}{4}-\frac{z}{8}$.
由图形可知当直线y=$\frac{3x}{4}-\frac{z}{8}$与圆A:(x-3)2+(y+2)2=25相切时,z分别取得最大值和最小值.
∴$\frac{|18+16-z|}{\sqrt{{6}^{2}+{8}^{2}}}=5$,解得z=-16或84.
∴z的最大值为84,最小值为-16.
故选:A.
点评 本题考查了平面向量的数量积运算,简单的线性规划,根据可行域寻找最优解的位置是解题关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.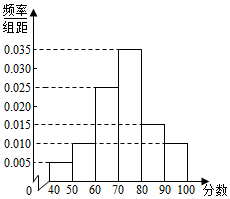 某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
 某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )| A. | 250 | B. | 200 | C. | 150 | D. | 100 |
20.若2cos2α=sin($\frac{π}{4}$-α),且α∈($\frac{π}{2}$,π),则sin2α的值为( )
| A. | -$\frac{7}{8}$ | B. | -$\frac{\sqrt{15}}{8}$ | C. | 1 | D. | $\frac{\sqrt{15}}{8}$ |
 已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=$\sqrt{3}$,如图所示,H为AO的中点.
已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=$\sqrt{3}$,如图所示,H为AO的中点.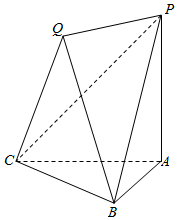 如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.