��Ŀ����
����Ŀ��С�����������ʱ��ȥ���Σ�����ΪС���ṩ�ĸ����㣬��կ����̩ɽ������ɽ������ɽ��С����������ѧ����ѧ֪ʶ�ƶ�һ������������ȥ�ĸ����㣺����ͼ������ ![]() ��ֱ��
��ֱ�� ![]() ���ڵ�
���ڵ� ![]() ����
���� ![]() Ϊ��㣬�ٴ�����
Ϊ��㣬�ٴ����� ![]() ����ȡ������ֱ�Ϊ�յ�õ�������������������������������Ϊ
����ȡ������ֱ�Ϊ�յ�õ�������������������������������Ϊ ![]() ����
���� ![]() ȥ��կ������
ȥ��կ������ ![]() ȥ̩ɽ����
ȥ̩ɽ���� ![]() ȥ����ɽ��
ȥ����ɽ�� ![]() ȥ����ɽ��
ȥ����ɽ��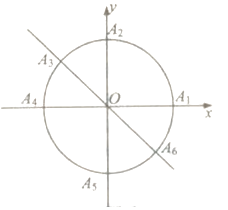
��1������ ![]() ������������ȡ������ֱ�Ϊ�յ�õ������������ֱ���С��ȥ��կ���ĸ��ʺͲ�ȥ̩ɽ�ĸ��ʣ�
������������ȡ������ֱ�Ϊ�յ�õ������������ֱ���С��ȥ��կ���ĸ��ʺͲ�ȥ̩ɽ�ĸ��ʣ�
��2��������������С�������� ![]() ��ȡ��
��ȡ�� ![]() ��Ϊ�������յ㣬��С������ȥ����ɽ����
��Ϊ�������յ㣬��С������ȥ����ɽ���� ![]() ������
������ ![]() ���˶�������
���˶������� ![]() ������Ϊ
������Ϊ ![]() ����
���� ![]() �����ֵ��
�����ֵ��
���𰸡�
��1���⣺�������֪�õ�������Ϸ�ʽ���У�
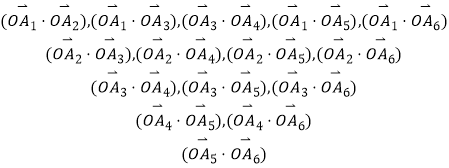
��15��
���¼���ȥ��կ����=B������ȥ̩ɽ��=C
��ȥ��կ������>0�� ![]()
��4��
![]()
ȥ̩ɽ��=0�� ![]()
��4��
![]()
��2���⣺�����⣺С��ȥ����ɽ�� ![]()
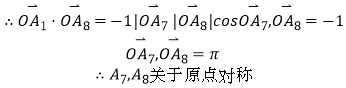
�ʿ��� ![]()
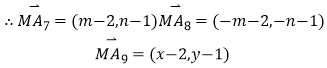
![]()
��ʽ�������壺Բ ![]() �ϵĵ���㣨6��3���ľ���
�ϵĵ���㣨6��3���ľ���
��ʽ�����ֵ���� ![]() ��������ֵ����Բ��
��������ֵ����Բ�� ![]() �ľ����ټӰ뾶
�ľ����ټӰ뾶
�� ![]()
���� ![]()
��������(1)�������г����п��ܵ��¼���Ϲŵ������ʽ����ø��ʡ�(2)���������������������������㹫ʽ�ɵó�A7,A8����ԭ��Գƣ����������������ϵ��������������͵�ģ��ΪԲ x2 + y2 = 1 �ϵĵ���㣨6��3���ľ��룬�ɼ�������ɵõ���ʽ�����ֵ���� ( x , y ) �� ( 6 , 3 ) ��������ֵ����Բ�� ( 0 , 3 ) �� ( 6 , 3 ) �ľ����ټӰ뾶��������ֵ����������
�����㾫����������Ĺؼ�����������Բ������λ�ù�ϵ�����֪ʶ������Բ�͵��λ�ù�ϵ���Ե�P��ԲO��Ϊ������P��һ�㣬��PO�ǵ㵽Բ�ĵľ��룩��P�ڡ�O�⣬PO��r��P�ڡ�O�ϣ�PO��r��P�ڡ�O�ڣ�PO��r��