题目内容
要获得某项英语资格证书必须依次通过听力和笔试两项考试,只有听力成绩合格时,才可继续参加笔试的考试.已知听力和笔试各只允许有一次不考机会,两项成绩均合格方可获得证书.现某同学参加这项证书考试,根据以往模拟情况,听力考试成绩每次合格的概率均为 ,笔试考试成绩每次合格的概率均为
,笔试考试成绩每次合格的概率均为 ,假设各次考试成绩合格与否均互不影响.
,假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)求他恰好补考一次就获得证书的概率;
(3)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求参加考试次数ξ的分布列和期望值.
解:设“听力第一次考试合格”为事件A1,“听力补考合格”为事件A2;“笔试第一次考试合格”为事件B1“笔试补考合格”为事件B2.(1分)
(1)不需要补考就获得证书的事件为A1•B1,注意到A1与B1相互独立,
则P(A1•B1)=P(A1)×P(B1)= ×
× =
= .A1•B1
.A1•B1
答:该考生不需要补考就获得证书的概率为 .(3分)
.(3分)
(2)恰好补考一次的事件是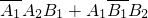 (4分)
(4分)
则P(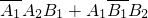 )=P(
)=P(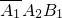 )+P(
)+P( )
)
=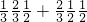 =
=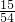 =
= (7分)
(7分)
(3)由已知得,ξ=2,3,4,(8分)
注意到各事件之间的独立性与互斥性,可得
P(ξ=2)=P(A1•B1)+P(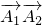 )=
)= ×
× +
+ ×
× =
= +
+ =
= (10分)
(10分)
P(ξ=3)=P(A1•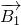 •
•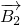 )+P(
)+P(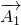 •A2•B2)=
•A2•B2)=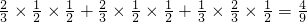 (12分)
(12分)
P(ξ=4)=P(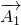 •A2•
•A2•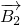 •B2)+P(
•B2)+P(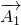 •A2•
•A2•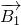 •
•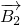 )=
)= ×
×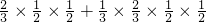 =
= +
+ =
= (13分)
(13分)
参加考试次数ξ的期望值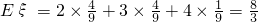 (14分)
(14分)
分析:设“听力第一次考试合格”为事件A1,“听力补考合格”为事件A2;“笔试第一次考试合格”为事件B1“笔试补考合格”为事件B2
(1)不需要补考就获得证书的事件为.A1•B1,且A1与B1相互独立,根据相互独立事件的概率公式可求
(2)他恰好补考一次就获得证书,即为事件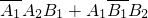 ,根据相互独立事件与互斥事件的概率公式可求
,根据相互独立事件与互斥事件的概率公式可求
(3)由已知得,ξ=2,3,4
而ξ=2即为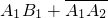 ξ=3 即为 A1•
ξ=3 即为 A1•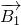 •
•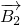 +
+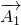 •A2•B2
•A2•B2
ξ=4,即为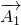 •A2•
•A2•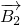 •B2+
•B2+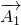
 •
•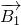 •
•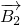
点评:本题主要考查了相互独立事件的 概率的求解公式的运用:若事件A,B相互独立,则A与 ,
,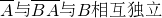 ;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查.
;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查.
(1)不需要补考就获得证书的事件为A1•B1,注意到A1与B1相互独立,
则P(A1•B1)=P(A1)×P(B1)=
 ×
× =
= .A1•B1
.A1•B1答:该考生不需要补考就获得证书的概率为
 .(3分)
.(3分)(2)恰好补考一次的事件是
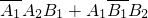 (4分)
(4分)则P(
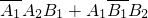 )=P(
)=P(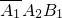 )+P(
)+P( )
)=
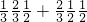 =
=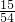 =
= (7分)
(7分)(3)由已知得,ξ=2,3,4,(8分)
注意到各事件之间的独立性与互斥性,可得
P(ξ=2)=P(A1•B1)+P(
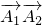 )=
)= ×
× +
+ ×
× =
= +
+ =
= (10分)
(10分)P(ξ=3)=P(A1•
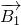 •
•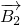 )+P(
)+P(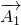 •A2•B2)=
•A2•B2)=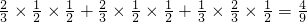 (12分)
(12分)P(ξ=4)=P(
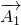 •A2•
•A2•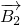 •B2)+P(
•B2)+P(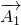 •A2•
•A2•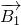 •
•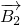 )=
)= ×
×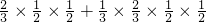 =
= +
+ =
= (13分)
(13分)参加考试次数ξ的期望值
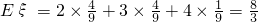 (14分)
(14分)分析:设“听力第一次考试合格”为事件A1,“听力补考合格”为事件A2;“笔试第一次考试合格”为事件B1“笔试补考合格”为事件B2
(1)不需要补考就获得证书的事件为.A1•B1,且A1与B1相互独立,根据相互独立事件的概率公式可求
(2)他恰好补考一次就获得证书,即为事件
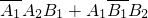 ,根据相互独立事件与互斥事件的概率公式可求
,根据相互独立事件与互斥事件的概率公式可求(3)由已知得,ξ=2,3,4
而ξ=2即为
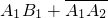 ξ=3 即为 A1•
ξ=3 即为 A1•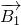 •
•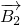 +
+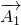 •A2•B2
•A2•B2ξ=4,即为
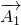 •A2•
•A2•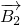 •B2+
•B2+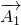
 •
•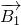 •
•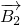
点评:本题主要考查了相互独立事件的 概率的求解公式的运用:若事件A,B相互独立,则A与
 ,
,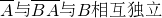 ;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查.
;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查. 
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
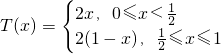
 x))和y=sin(
x))和y=sin( ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;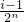 ,
,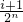 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(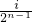 -x)恒成立.
-x)恒成立. =(m,n),
=(m,n), =(s,t),定义两个向量
=(s,t),定义两个向量 =(1,2),
=(1,2), =(-3,-4),则向量
=(-3,-4),则向量



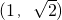
 ∈A,则称集合A为“完美集合”.在集合A{-1,1,2,3}的所有非空子集中任取-个集合,这个集合是“完美集合”的概率为
∈A,则称集合A为“完美集合”.在集合A{-1,1,2,3}的所有非空子集中任取-个集合,这个集合是“完美集合”的概率为 -
-


 ,切点到二面角棱的距离是1,则球的表面积是________,球的体积是________.
,切点到二面角棱的距离是1,则球的表面积是________,球的体积是________.