题目内容
已知f(x)=2012sinx+2011x3,且x∈(-1,1),若f(1-a)+f(1-a2)<0,则a的取值范围是
- A.(0,2)
- B.

- C.(-2,0)
- D.
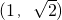
D
分析:在区间(-1,1)上,由f(-x)=-f(x)、f′(x)>0可知函数f(x)是奇函数且单调递增,由此可求出a的取值范围,进而选出答案.
解答:∵f(x)=2012sinx+2011x3,?x∈(-1,1),则f(-x)=-f(x),∴f(x)在区间(-1,1)上是奇函数;
又f′(x)=2012cosx+6033x2,x∈(-1,1),∴f′(x)>0,∴f(x)在区间(-1,1)上单调递增;
由f(1-a)+f(1-a2)<0,∴f(1-a)<-f(1-a2),∴f(1-a)<f(a2-1),
∴-1<1-a<a2-1<1,解之得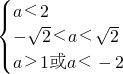 即
即 ,
,
所以a的取值范围是(1, ).
).
故选 D.
点评:本题考查了函数的奇偶性、单调性,充分理解函数的奇偶性、单调性是解决问题的关键.
分析:在区间(-1,1)上,由f(-x)=-f(x)、f′(x)>0可知函数f(x)是奇函数且单调递增,由此可求出a的取值范围,进而选出答案.
解答:∵f(x)=2012sinx+2011x3,?x∈(-1,1),则f(-x)=-f(x),∴f(x)在区间(-1,1)上是奇函数;
又f′(x)=2012cosx+6033x2,x∈(-1,1),∴f′(x)>0,∴f(x)在区间(-1,1)上单调递增;
由f(1-a)+f(1-a2)<0,∴f(1-a)<-f(1-a2),∴f(1-a)<f(a2-1),
∴-1<1-a<a2-1<1,解之得
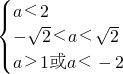 即
即 ,
,所以a的取值范围是(1,
 ).
).故选 D.
点评:本题考查了函数的奇偶性、单调性,充分理解函数的奇偶性、单调性是解决问题的关键.

练习册系列答案
相关题目
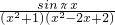 ,下列结论正确的是________.
,下列结论正确的是________.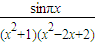 ,下列结论正确的是 .
,下列结论正确的是 .