题目内容
15.已知2sina+cosa=$\frac{\sqrt{10}}{2}$,则tan2a=$\frac{3}{4}$.分析 把已知等式两边平方,化为切函数,求出tana的值,代入倍角公式得答案.
解答 解:由2sina+cosa=$\frac{\sqrt{10}}{2}$,得
$(2sina+cosa)^{2}=\frac{5}{2}$,即$4si{n}^{2}a+4sinacosa+co{s}^{2}a=\frac{5}{2}$.
∴$\frac{4si{n}^{2}a+4sinacosa+co{s}^{2}a}{si{n}^{2}a+co{s}^{2}a}=\frac{5}{2}$,
∴$\frac{4ta{n}^{2}a+4tana+1}{ta{n}^{2}a+1}=\frac{5}{2}$.
则3tan2a+8tana-3=0.
解得:tana=-3或tana=$\frac{1}{3}$.
当tana=-3时,tan2a=$\frac{2tana}{1-ta{n}^{2}a}$=$\frac{3}{4}$;
当tana=$\frac{1}{3}$时,tan2a=$\frac{2tana}{1-ta{n}^{2}a}$=$\frac{3}{4}$.
综上,tan2a=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查三角函数的化简与求值,考查了计算能力,是中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
20.直接写出下列不等式的解集
$\left\{\begin{array}{l}{2-x<0}\\{1+x>5}\end{array}\right.$(4,+∞) x2>1(-∞,-1)∪(1,+∞).
$\left\{\begin{array}{l}{2-x<0}\\{1+x>5}\end{array}\right.$(4,+∞) x2>1(-∞,-1)∪(1,+∞).
7.设点M为中心在原点,对称轴为x轴的椭圆上的点,M到两个焦点的距离之和为12,椭圆的焦距为8,则该椭圆的标准方程是( )
| A. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{16}$=1 | D. | $\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{20}$=1 |
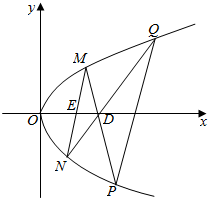 如图,在平面直角坐标系中,已知抛物线C:y2=2px(p>0).设点D(n,0),E(m,0).M为抛物线C上的动点(异于顶点),连接ME并延长交抛物线C于点N,连接MD、ND并延长交抛物线C于点P、Q,连接PQ.设直线MN、PQ的斜率存在且分别为k1,k2.
如图,在平面直角坐标系中,已知抛物线C:y2=2px(p>0).设点D(n,0),E(m,0).M为抛物线C上的动点(异于顶点),连接ME并延长交抛物线C于点N,连接MD、ND并延长交抛物线C于点P、Q,连接PQ.设直线MN、PQ的斜率存在且分别为k1,k2.