题目内容
如图，在等腰三角形ABC中，∠ACB＝120˚，BC＝AC＝3，点D在线段AB上.
⑴若
，求BD的长;
⑵若点E在线段DA上，且∠DCE＝30˚，问:当∠DCB取何值时，△CDE的面积最小?并求出面积的最小值.
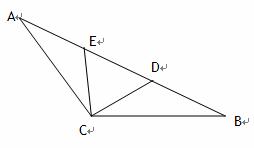
解⑴在△CDB中，∠CBD＝30˚，BC＝3，，由余弦定理，
得
，……………………2分
即
，解得，
.……………………4分
⑵设∠DCB＝
，
，在△CDB中，由正弦定理，得
，
即
，同理
，……………………6分
所以，
…………………………10分
∵，∴
.
∴当
时，
的最小值为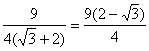
.…………12分
练习册系列答案
相关题目
如图，在等腰直角三角形ABC中，则AM＜AC的概率为（ ）
（2013•徐州一模）如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且
．
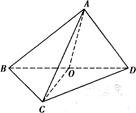
时，求证：AO⊥平面BCD；
的大小为
时，求二面角
的正切值．
如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且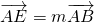
，
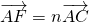，其中m，n∈（0，1）．若EF，BC的中点分别为M，N，且m+4n=1，则
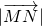的最小值为________．
如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且
，
，其中m，n∈（0，1）．若EF，BC的中点分别为M，N，且m+4n=1，则
的最小值为 ．