题目内容
当两个向量 ,
, 不共线时,求证:
不共线时,求证:
(1) <
< <
< ;(2)
;(2) <
<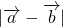 <
< .
.
证明:(1)|如图所示:设  =
= ,
, =
= ,以OA、OB为邻边作一个平行四边形OACB,
,以OA、OB为邻边作一个平行四边形OACB,
则 =
= ,
, =
= .△ABC中,∵AO-AC<OC,∴
.△ABC中,∵AO-AC<OC,∴ <
< .
.
∵OC<AO+AC∴ <
< .
.
综上, <
< <
< 成立.
成立.
(2)△AOB中,∵OA-OB<AB,∴ <
<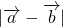 ,
,
∵AB<OA+OB,∴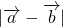 <
< ,综上,
,综上,
有 <
<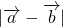 <
< 成立.
成立.

分析:(1)|如图:设 =
= ,
, =
= ,△ABC中,由AO-AC<OC,可得
,△ABC中,由AO-AC<OC,可得  <
< ;
;
由 OC<AO+AC 可得 <
< .
.
(2)△AOB中,由OA-OB<AB,可得 <
<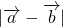 ; 由AB<OA+OB 可得
; 由AB<OA+OB 可得 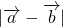 <
< .
.
点评:本题考查两个向量的和差的运算及其几何意义,三角形中,任意两边之和大于第三边,任意两边之差小于第三边,
体现了数形结合的数学思想.
 =
= ,
, =
= ,以OA、OB为邻边作一个平行四边形OACB,
,以OA、OB为邻边作一个平行四边形OACB,则
 =
= ,
, =
= .△ABC中,∵AO-AC<OC,∴
.△ABC中,∵AO-AC<OC,∴ <
< .
.∵OC<AO+AC∴
 <
< .
.综上,
 <
< <
< 成立.
成立.(2)△AOB中,∵OA-OB<AB,∴
 <
<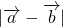 ,
,∵AB<OA+OB,∴
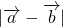 <
< ,综上,
,综上,有
 <
<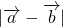 <
< 成立.
成立.
分析:(1)|如图:设
 =
= ,
, =
= ,△ABC中,由AO-AC<OC,可得
,△ABC中,由AO-AC<OC,可得  <
< ;
;由 OC<AO+AC 可得
 <
< .
.(2)△AOB中,由OA-OB<AB,可得
 <
<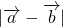 ; 由AB<OA+OB 可得
; 由AB<OA+OB 可得 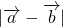 <
< .
.点评:本题考查两个向量的和差的运算及其几何意义,三角形中,任意两边之和大于第三边,任意两边之差小于第三边,
体现了数形结合的数学思想.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 ,
, 不共线时,求证:
不共线时,求证: <
< <
< ;(2)
;(2) <
< <
< .
.