题目内容
设F1、F2是椭圆
＝1的两个焦点，P是椭圆上的点，且|PF1|∶|PF2|＝2∶1，则△PF1F2的面积等于________．
答案：4
解析：
解析：
|
设椭圆的长轴、短轴的长及焦距分别为2a、2b、2c，由方程可知a＝3，b＝2，c＝ |
，故|PF1|＋|PF2|＝2a＝6．又∵|PF1|∶|PF2|＝2∶1，∴|PF1|＝4，|PF2|＝2．而|F1F2|＝2c＝
，故在△PF1F2中，有|PF1|2＋|PF2|2＝|F1F2|2，∴△PF1F2为直角三角形，两直角边长分别为4和2．故△PF1F2的面积为
×4×2＝4．
练习册系列答案
相关题目
＝1(a＞b＞0)的两个焦点，P是以F1、F2为直径的圆与椭圆的一个交点，且∠PF1F2＝5∠PF2F1，则此椭圆的离心率的倒数是
＝1的两个焦点，P是椭圆上一点，且|PF1|－|PF2|＝1，则cos∠F1PF2＝________．
＝1的焦点，P是其上一点且|PF1|－|PF2|＝1，则tan∠F1PF2＝________．
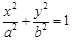(a＞b＞0)的左、右焦点，过F1的直线
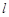与
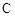交于A，B两点．若AB⊥AF2，|AB|:|AF2|＝3:4，则椭圆的离心率为
．