题目内容
对于使x2-2x≥M成立的所有常数M中,我们把M的最大值-1,称为函数x2-2x的“下确界”,若x,y,z∈R+,且x-y+2z=0,
的“下确界”为( )
| y2 |
| xz |
| A、8 | B、6 | C、4 | D、1 |
分析:利用x-y+2z=0,化简表达式
,利用基本不等式求函数的最值,即可求得函数的“下确界”.
| y2 |
| xz |
解答:解:∵x-y+2z=0,
∴y=x+2z,
表达式
,可化为
=
≥
=8.
(当且仅当2z=x时取等号)
∴
≥8.
∴
的“下确界”等于8,
故选:A.
∴y=x+2z,
表达式
| y2 |
| xz |
| y2 |
| xz |
| (x+2z)2 |
| xz |
(2
| ||
| xz |
(当且仅当2z=x时取等号)
∴
| y2 |
| xz |
∴
| y2 |
| xz |
故选:A.
点评:本题考查新定义,考查基本不等式的运用,解题的关键是利用基本不等式求函数的最值,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
对于使-x2+2x≤M成立的所有常数M中,我们把M的最小值1叫做-x2+2x的上确界,若a,b∈R+,且a+b=1,则-
-
的上确界为( )
| 1 |
| 2a |
| 2 |
| b |
A、
| ||
B、-
| ||
C、-
| ||
| D、-4 |
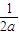 -
-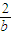 的上确界为 .
的上确界为 .