题目内容
二面角α–EF–β的大小为120°,A是它内部的一点AB⊥α,AC⊥β,B,C分别为垂足.
(1)求证:平面ABC⊥β;
(2)当AB=4cm,AC=6cm,求BC的长及A到EF的距离.

(1)∵AB⊥α,EF![]() α,∴EF⊥AB,同理EF⊥AC,AB,AC是两条相交直线,∴ EF⊥平面ABC,∵ EF
α,∴EF⊥AB,同理EF⊥AC,AB,AC是两条相交直线,∴ EF⊥平面ABC,∵ EF![]() α,EF
α,EF![]() β,∴ 平面ABC⊥平面α,平面ABC⊥平面β。
β,∴ 平面ABC⊥平面α,平面ABC⊥平面β。
(2)设平面ABC与EF交于点D,连结BD,CD,则BD,CD![]() 平面ABC,∵EF⊥平面ABC,∴ EF⊥BC,EF⊥DC,∠BDC是二面角α–EF–β的平面角,∠BCD=120°,A,B,C,D在同一平面内,且∠ABD=∠ACD=90°,
平面ABC,∵EF⊥平面ABC,∴ EF⊥BC,EF⊥DC,∠BDC是二面角α–EF–β的平面角,∠BCD=120°,A,B,C,D在同一平面内,且∠ABD=∠ACD=90°,
∴∠BAC=60°,当AB=4 cm, AC=6 cm时,
BC=![]()
又∵ A,B,C,D共圆,∵AD是直径。∵ EF⊥平面ABC,AD![]() 平面ABC,
平面ABC,
∴ AD⊥EF,即AD是A到EF的距离,由正弦定理,得AD=![]() =
=![]() (cm)
(cm)

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
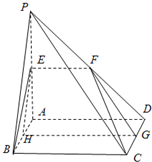 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G,H分别是线段PA,PD,CD,AB的中点.
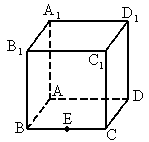
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G,H分别是线段PA,PD,CD,AB的中点.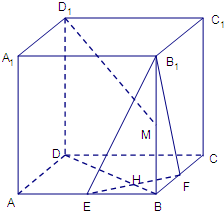 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB和BC的中点,EF与BD相交于点H,M为BB1中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB和BC的中点,EF与BD相交于点H,M为BB1中点. (2013•广元二模)如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2
(2013•广元二模)如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2 中,点E是棱BC的中点,点F是棱CD上的动点.
中,点E是棱BC的中点,点F是棱CD上的动点. E⊥平面A
E⊥平面A F;
F;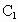 -EF-A的大小(结果用反三角函数值表示).
-EF-A的大小(结果用反三角函数值表示).
 中,点E是棱BC的中点,点F是棱CD上的动点.
中,点E是棱BC的中点,点F是棱CD上的动点.
 E⊥平面A
E⊥平面A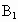 F;
F;
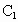 -EF-A的大小(结果用反三角函数值表示).
-EF-A的大小(结果用反三角函数值表示).