题目内容
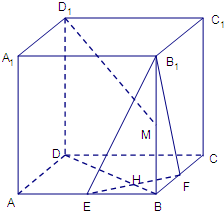 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB和BC的中点,EF与BD相交于点H,M为BB1中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是AB和BC的中点,EF与BD相交于点H,M为BB1中点.①求二面角B1-EF-B的大小;
②求证:D1M⊥平面B1EF;
③求点D1到平面B1EF的距离.
分析:①连接B1H,由等腰三角形“三线合一”的性质可得EF⊥BH,由正方体的几何特征,可得B1H⊥EF,则∠B1HB是二面角B1-EF-B的平面角,解三角形B1HB,即可得到二面角B1-EF-B的大小.
②由BD⊥EF,D1M在平面ABCD的射影为BD,由三垂线定理可得D1M⊥EF,连接A1M,易证得D1M⊥B1E,由线面垂直的判定定理,可得D1M⊥平面B1EF;
③由②中结论可得D1N⊥平面B1EF,则D1N的长即为D1到平面B1EF的距离,连接B1D1,解Rt△B1D1M即可得到D1N的长,进而得到点D1到平面B1EF的距离.
②由BD⊥EF,D1M在平面ABCD的射影为BD,由三垂线定理可得D1M⊥EF,连接A1M,易证得D1M⊥B1E,由线面垂直的判定定理,可得D1M⊥平面B1EF;
③由②中结论可得D1N⊥平面B1EF,则D1N的长即为D1到平面B1EF的距离,连接B1D1,解Rt△B1D1M即可得到D1N的长,进而得到点D1到平面B1EF的距离.
解答: 解:①连接B1H,∵E、F分别是AB、BC的中点,∴EF⊥BH
解:①连接B1H,∵E、F分别是AB、BC的中点,∴EF⊥BH
又BB1⊥平面ABCD,∴BH是B1H在平面ABCD的射影,∴B1H⊥EF
∴∠B1HB是二面角B1-EF-B的平面角--------------------------------------------2′
显然tan∠B1HB=
=
=
=2
-----------------------------4′
∴∠B1HB=arctan2
即二面角B1-EF-B的大小为arctan2
-------------------------------------------5′
②∵D1M在平面ABCD的射影为BD又BD⊥EF,∴D1M⊥EF--------------------7′
连接A1M,D1M在平面A1ABB1的射影为A1M
由△A1M B1≌△B1BE知A1M⊥B1E
∴D1M⊥B1E----------------------------------------------------------------------------------9′
又B1E∩EF=E,∴D1M⊥平面B1EF---------------------------------------------------10′
(若用向量法证,相应给分)
③设B1H∩D1M于N,由②知D1N⊥平面B1EF
∴D1N的长即为D1到平面B1EF的距离
连接B1D1,则在Rt△B1D1M中
D1N=
=
=
a-----------------------------------------------------14′
 解:①连接B1H,∵E、F分别是AB、BC的中点,∴EF⊥BH
解:①连接B1H,∵E、F分别是AB、BC的中点,∴EF⊥BH又BB1⊥平面ABCD,∴BH是B1H在平面ABCD的射影,∴B1H⊥EF
∴∠B1HB是二面角B1-EF-B的平面角--------------------------------------------2′
显然tan∠B1HB=
| B1B |
| BH |
| B1B | ||
|
| B1B | ||||
|
| 2 |
∴∠B1HB=arctan2
| 2 |
即二面角B1-EF-B的大小为arctan2
| 2 |
②∵D1M在平面ABCD的射影为BD又BD⊥EF,∴D1M⊥EF--------------------7′
连接A1M,D1M在平面A1ABB1的射影为A1M
由△A1M B1≌△B1BE知A1M⊥B1E
∴D1M⊥B1E----------------------------------------------------------------------------------9′
又B1E∩EF=E,∴D1M⊥平面B1EF---------------------------------------------------10′
(若用向量法证,相应给分)
③设B1H∩D1M于N,由②知D1N⊥平面B1EF
∴D1N的长即为D1到平面B1EF的距离
连接B1D1,则在Rt△B1D1M中
D1N=
| D1B12 |
| D1M |
| 2a2 | ||||
|
| 4 |
| 3 |
点评:本题考查的知识点二面角的平面角及求法,直线与平面垂直的判定,点到平面之间的距离,其中①的关键是证得∠B1HB是二面角B1-EF-B的平面角,②的关键是证得D1M⊥EF且D1M⊥B1E,③是证得D1N的长即为D1到平面B1EF的距离.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





