Question

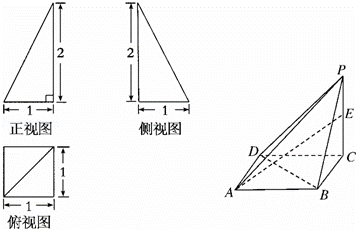
已知四棱锥P﹣ABCD的三视图和直观图如图：

（1）求四棱锥P﹣ABCD的体积；

（2）若E是侧棱PC上的动点，是否不论点E在何位置，都有BD⊥AE？证明你的结论．

（3）若F是侧棱PA上的动点，证明：不论点F在何位置，都不可能有BF⊥平面PAD．

Answer 1

考点：

直线与平面垂直的判定；由三视图还原实物图．

专题：

空间位置关系与距离．

分析：

（1）由三视图可知，四棱锥中，PC⊥底面ABCD，底面ABCD是边长为1的正方形，PC=2，再利用三棱锥的体积计算公式就看得出V_P﹣ABCD=•PC•S_底．

（2）不论点E在何位置，都有BD⊥AE成立．连接AC，可得BD⊥AC，利用线面垂直的性质可得BD⊥PC，从而得到BD⊥平面PAC，即可得出结论；

（3）用反证法：假设BF⊥平面PAD，利用线面垂直的性质定理可得BF⊥AD．进而得到AD⊥平面PBC，可得AD⊥PA．利用PC⊥平面ABCD，可得AD⊥PC，于是AD⊥平面PDC，可得AD⊥PD．于是得到PA∥PD与PA∩PD=P矛盾即可．

解答：

（1）解：由三视图可知，四棱锥中，PC⊥底面ABCD，底面ABCD是边长为1的正方形，PC=2，

∴V_P﹣ABCD=•PC•S_底=×2×1=．

（2）不论点E在何位置，都有BD⊥AE成立．

证明：连接AC，由正方形ABCD可得BD⊥AC，

又∵PC⊥底面ABCD，

∴BD⊥PC，

又AC∩PC=C，

∴BD⊥平面PAC，

当E在PC上运动时，AE⊂平面PAC，

∴BD⊥AE恒成立．

（3）用反证法：假设BF⊥平面PAD，∵DA⊂平面PAD，∴BF⊥AD．

又AD⊥AB，AB∩BF=B，∴AD⊥平面PAB，∴AD⊥PA．

∵PC⊥平面ABCD，∴AD⊥PC．

∵AD⊥DC，DC∩PC=C，∴AD⊥平面PDC，∴AD⊥PD．

∴PD∥PA与PD∩PA=P项矛盾．

∴BF不可能垂直于平面PAD．

点评：

熟练掌握线面垂直的判定与性质、正方形的性质、三棱锥的体积计算公式、反证法等是解题的关键．