Question

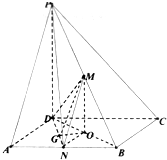（2011•重庆二模）如图，已知四棱锥P-ABCD的底面是边长为4的正方形，PD⊥ABCD，设PD=4

3

，M、N分别是PB、AB的中点．
（Ⅰ）求异面直线MN与PD所成角的大小；
（Ⅱ）求二面角M-DN-C的平面角的正切值．

Answer 1

分析：（I）连接BD，并取其中点O，连接MO，NO，MN，DN，PN，可得∠NMO为异面直线MN与PD所成角，且MO⊥平面ABCD，求出NO，MO，即可求异面直线MN与PD所成角的大小；
（Ⅱ）过点O作OG⊥DN于G，连接MG，则∠MGO是二面角M-DN-C的平面角，从而可求二面角M-DN-C的平面角的正切值．

解答：解：（I）如图，连接BD，并取其中点O，连接MO，NO，MN，DN，PN，
则MO∥PD，且MO=

1

2

PD
∴∠NMO为异面直线MN与PD所成角，且MO⊥平面ABCD
∴MO⊥NO，MO=2

3

，NO=

1

2

AD=2
∴tan∠NMO=

NO

MO

=

2

2 3

=

3

3

∴∠NMO=

π

6

∴异面直线MN与PD所成角为

π

6

；
（II）过点O作OG⊥DN于G，连接MG．
∵MO⊥平面ABCD，∴OG是MG在平面ABCD上的射影，
由三垂线定理得：MG⊥DN，∴∠MGO是二面角M-DN-C的平面角．
在△DON中，由面积相等得：

1

2

•DN•OG=

1

8

S△ABCD=2
∴OG=

2

5

，
∵OM=

1

2

PD=2

3

，
∴tan∠MGO=

OM

OG

=

15

∴二面角M-DN-C的平面角的正切值

15

．

点评：本题考查空间角，考查学生分析解决问题的能力，正确作出空间角是关键．