题目内容
17.求函数f(x)=$\frac{x}{a}$+$\frac{a}{x}$(a>0)在x∈[1,2]的最小值.分析 先用基本不等式得出函数单调区间的分界点,再对参数a分三类讨论,求出各范围的最小值,最后再综合.
解答 解:根据基本不定式,$\frac{x}{a}$+$\frac{a}{x}$≥2$\sqrt{\frac{x}{a}•\frac{a}{x}}$=2,
当且仅当:x=a时,取“=”,
所以,函数f(x)在[1,2]上的最小值需讨论如下:
①当0<a<1时,函数f(x)在[1,2]上单调单调递增,
所以f(x)min=f(1)=a+$\frac{1}{a}$;
②当1≤a≤2时,f(x)的最小值已由基本不等式得出,
即f(x)min=f(a)=2;
③当a>2时,函数f(x)在[1,2]上单调单调递减,
所以,f(x)min=f(2)=$\frac{2}{a}$+$\frac{a}{2}$.
综合以上讨论得,f(x)min=$\left\{\begin{array}{l}{a+\frac{1}{a},a∈(0,1)}\\{2,a∈[1,2]}\\{\frac{2}{a}+\frac{a}{2},a∈(2,+∞)}\end{array}\right.$.
点评 本题主要考查了运用基本不等式求最值,以及双勾函数性质的运用,还体现了分类讨论的思想,属于中档题.

练习册系列答案
相关题目
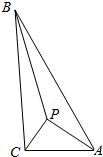 如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.
如图,在△ABC中,∠C=90°,P为三角形内一点,且S△PAB=S△PBC=S△PCA,求证:|PA|2+|PB|2=5|PC|2.