题目内容
如图，P是边长为3的正方形ABCD所在平面外的一点，PD⊥平面ABCD，O、E、F分别是AC、PA、PB的中点． 求证：平面EFO∥ 平面PDC；
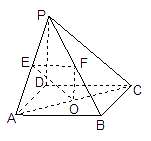
证明EO∥平面PCD
解析:
证明：如图所示，在△PAB中，E、F分别为PA、PB的中点
∴ EF∥AB,
又∵四边形ABCD是正方形，∴ AB∥CD, ∴ EF∥CD
又∵CD
平面PCD，EF
平面PCD，∴ EF∥平面PCD
在△PAC中，E、O分别为PA、AC的中点
∴ EO∥PC
又∵PC平面PCD，EO平面PCD，∴ EO∥平面PCD
又∵EF∩EO=E， EF平面EFO， EO平面EFO
∴平面EFO∥平面PDC
练习册系列答案
相关题目
如图，ABCD是边长为a的菱形，且∠BAD=60°，△PAD为正三角形，且面PAD⊥面ABCD．
AB
AB
AB，剪掉△MNB，以DM、DN为折痕，将DA与DC重合于点P，可以构成一个无底的三棱锥，那么这个三棱锥的体积为___________.