题目内容
“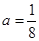 ”是“对任意的正数
”是“对任意的正数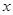 ,
,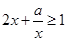 ”的 ( )
”的 ( )
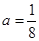 ”是“对任意的正数
”是“对任意的正数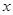 ,
,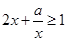 ”的 ( )
”的 ( )| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条 |
A
分析:根据基本不等式,我们可以判断出“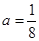 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+ ≥1”?“a=
≥1”?“a=
”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a= ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,2x+ ≥1”一定成立,
≥1”一定成立,
即“a= ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ≥1”为真命题;
≥1”为真命题;
而“对任意的正数x,2x+ ≥1的”时,可得“a≥
≥1的”时,可得“a≥ ”
”
即“对任意的正数x,2x+ ≥1”?“a=
≥1”?“a= ”为假命题;
”为假命题;
故“a= ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+ ≥1的”充分不必要条件
≥1的”充分不必要条件
故选A
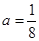 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+ ≥1”?“a=
≥1”?“a= ”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=
 ”时,由基本不等式可得:
”时,由基本不等式可得:“对任意的正数x,2x+
 ≥1”一定成立,
≥1”一定成立,即“a=
 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ≥1”为真命题;
≥1”为真命题;而“对任意的正数x,2x+
 ≥1的”时,可得“a≥
≥1的”时,可得“a≥ ”
”即“对任意的正数x,2x+
 ≥1”?“a=
≥1”?“a= ”为假命题;
”为假命题;故“a=
 ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+ ≥1的”充分不必要条件
≥1的”充分不必要条件故选A

练习册系列答案
相关题目
 (p或q)”为假命题,则 ( )
(p或q)”为假命题,则 ( ) .
.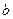 .
.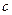
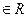 ,且
,且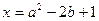 ,
,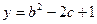 ,
,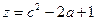 ,则
,则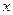 .
.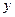 .
.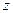 中至少有一个不小于0.
中至少有一个不小于0.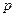 :函数
:函数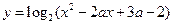 的定义域为R;命题
的定义域为R;命题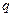 :方程
:方程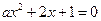 有两个不相等的负数根,若
有两个不相等的负数根,若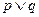 是假命题,求实数
是假命题,求实数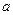 的取值范围
的取值范围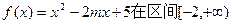 上是增函数 命题q:
上是增函数 命题q: 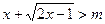 恒成立。若p或q为真命题,命题p且q为假,
恒成立。若p或q为真命题,命题p且q为假, )是极小值,f(
)是极小值,f(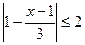 ,q:
,q: 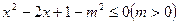 ,若
,若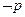 是
是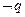 的必要不
的必要不