题目内容
【题目】已知非零向量 ![]() ,
, ![]() 满足|
满足| ![]() |=1,且(
|=1,且( ![]() ﹣
﹣ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() .
.
(1)求| ![]() |;
|;
(2)当 ![]()
![]() =-
=- ![]() 时,求向量
时,求向量 ![]() 与
与 ![]() +2
+2 ![]() 的夹角θ的值.
的夹角θ的值.
【答案】
(1)解:因为( ![]() ﹣
﹣ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() ,即
,即 ![]() =
= ![]() ,即|
,即| ![]() |2﹣|
|2﹣| ![]() |2=
|2= ![]() ,
,
所以,| ![]() |2=|
|2=| ![]() |2﹣
|2﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]() ,故|
,故| ![]() |=
|= ![]()
(2)解:因为| ![]() |2 =|
|2 =| ![]() |2+4
|2+4 ![]() +|2
+|2 ![]() |2=1﹣1+1=1,故|
|2=1﹣1+1=1,故| ![]() |=1.
|=1.
又因为 ![]() (
( ![]() )=|
)=| ![]() |2+2
|2+2 ![]() =1﹣
=1﹣ ![]() =
= ![]() ,
,
∴cos θ= 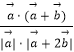 ═
═ ![]() ,
,
又0°≤θ≤180°,故θ=60°
【解析】(1)由( ![]() ﹣
﹣ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() 可得
可得 ![]() =
= ![]() ,再由|
,再由| ![]() |=1求得|
|=1求得| ![]() |2=
|2= ![]() ,从而求得|
,从而求得| ![]() |.(2)由
|.(2)由 ![]()
![]() =-
=- ![]() 求得|
求得| ![]() |=1,再求得
|=1,再求得 ![]() (
( ![]() )=1,利用两个向量的夹角公式求得cosθ的值,即可求得θ的值.
)=1,利用两个向量的夹角公式求得cosθ的值,即可求得θ的值.
【考点精析】根据题目的已知条件,利用数量积表示两个向量的夹角的相关知识可以得到问题的答案,需要掌握设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则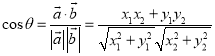 .
.

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.