题目内容
过抛物线E:y2=4x焦点F的直线l与E交与不同两点A(x1,y1),B(x2,y2),则| 1 |
| x1 |
| 4 |
| x2 |
分析:先根据抛物线方程求得焦点坐标,进而根据点斜式设直线l的方程,与抛物线方程联立消去y,根据韦达定理求得x1x2的值,进而根据均值不等式
+
≥2
求得答案.
| 1 |
| x1 |
| 4 |
| x2 |
|
解答:解:抛物线y2=4x,焦点坐标为(1,0),设直线l的方程为y=k(x-1),
则
消去y得k2x2-(2k2+4)x+k2=0
∴x1x2=1
∵x1>0,x2>0
∴
+
≥2
=4当且仅当4x1=x2时取等号;
故答案为4.
则
|
∴x1x2=1
∵x1>0,x2>0
∴
| 1 |
| x1 |
| 4 |
| x2 |
|
故答案为4.
点评:本题主要考查了直线与圆锥曲线的综合问题.解此类题常需要把直线和圆锥曲线方程联立.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 设直线过抛物线C:y2=2px(p>0)的焦点F,且交C于点M,N,设
设直线过抛物线C:y2=2px(p>0)的焦点F,且交C于点M,N,设 (2012•莆田模拟)如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论:
(2012•莆田模拟)如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论:
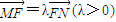 .
.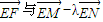 的夹角为定值.
的夹角为定值.