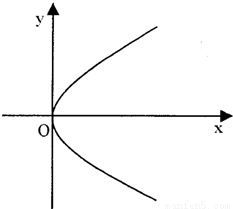
题目内容
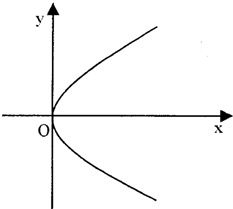 设直线过抛物线C:y2=2px(p>0)的焦点F,且交C于点M,N,设
设直线过抛物线C:y2=2px(p>0)的焦点F,且交C于点M,N,设| MF |
| FN |
(I)若p=2,λ=4,求MN所在的直线方程;
(II)若p=2,4≤λ≤9,求直线MN在y轴上截距的取值范围;
(III)抛物线C的准线l与x轴交于点E,求证:
| EF |
| EM |
| EN |
分析:(I)p=2时,抛物线y2=4x,F(1,0),设M(x1,y1),N(x2,y2),
=λ
(λ>0)得(1-x1,y1)=λ(x2-1,-y2),即
,由此能求出MN所在的直线方程.
(II)由p=2得直线MN方程为(λ-1)y=2
(x-1)或(λ-1)y=-2
(x-1),由此能求出直线MN在y轴上截距的取值范围.
(III)设M,N在直线l上的射影为M’,N’,则有
=
+
,
=
+
,由
=λ
,知
-λ
=
-λ
,由此能求出
与
-λ
的夹角为定值90°.
| MF |
| FN |
|
(II)由p=2得直线MN方程为(λ-1)y=2
| λ |
| λ |
(III)设M,N在直线l上的射影为M’,N’,则有
| EM |
| EM‘ |
| M’M |
| EN |
| EN‘ |
| N’N |
| MM‘ |
| NN’ |
| EM |
| EN |
| EM’ |
| EN‘ |
| EF |
| EM |
| EN |
解答:解:(I)p=2时,抛物线y2=4x,F(1,0),设M(x1,y1),N(x2,y2),
=λ
(λ>0)得(1-x1,y1)=λ(x2-1,-y2),即
由②得y12=λ2y22,∵y12=4x1,y22=4x2,∴x1=λ2x2.③
联立①、③解得x2=
,x1=λ,依题意有λ>0.
(II)由(I)及p=2得直线MN方程为(λ-1)y=2
(x-1)或(λ-1)y=-2
(x-1),
当λ∈[4,9]时,MN在y轴上的截距为
或-
,
令f(x)=
,则f′(x)=
<0
(III)设M,N在直线l上的射影为M’,N’,则有
=
+
,
=
+
,
由于
=λ
,∴
-λ
=
-λ
,
∵
⊥(
-λ
),∴
⊥(
-λ
),
∴
与
-λ
的夹角为定值90°.
| MF |
| FN |
|
由②得y12=λ2y22,∵y12=4x1,y22=4x2,∴x1=λ2x2.③
联立①、③解得x2=
| 1 |
| λ |
|
(II)由(I)及p=2得直线MN方程为(λ-1)y=2
| λ |
| λ |
当λ∈[4,9]时,MN在y轴上的截距为
2
| ||
| λ-1 |
2
| ||
| λ-1 |
令f(x)=
2
| ||
| x-1 |
| -x-1 | ||
|
|
(III)设M,N在直线l上的射影为M’,N’,则有
| EM |
| EM‘ |
| M’M |
| EN |
| EN‘ |
| N’N |
由于
| MM‘ |
| NN’ |
| EM |
| EN |
| EM’ |
| EN‘ |
∵
| EF |
| EM‘ |
| EN’ |
| EF |
| EM |
| EN |
∴
| EF |
| EM |
| EN |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 .
.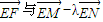 的夹角为定值.
的夹角为定值.