题目内容
解关于x的不等式
＜x．
| x2+3 |
| x-a |
考点：其他不等式的解法
专题：计算题,不等式的解法及应用
分析：原不等式等价于（ax+3）（x-a）＜0．分类讨论，即可得出结论．
解答：
解：原不等式等价于（ax+3）（x-a）＜0．
（1）a=0时，解集为（-∞，0）；
（2）a≠0时，有两根a和-
．
①a＜0时，a＜-
，解集为（-∞，a）∪（-
，+∞）；
②a＞0时，a＞-
，解集为（-
，a）．
（1）a=0时，解集为（-∞，0）；
（2）a≠0时，有两根a和-
| 3 |
| a |
①a＜0时，a＜-
| 3 |
| a |
| 3 |
| a |
②a＞0时，a＞-
| 3 |
| a |
| 3 |
| a |
点评：本题考查不等式的解法，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
在四边形ABCD中，
-
+
等于（ ）
| AB |
| AC |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={1，2，3，4，5}，集合B={1，3，5}，则集合A∩B=（ ）
| A、{2，4} |
| B、{1，2，3} |
| C、{1，3，5} |
| D、{1，2，3，4，5} |
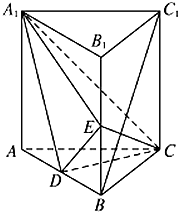如图，直棱柱ABC-A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB=