题目内容
已知函数![]() 是定义在
是定义在![]() 上的单调奇函数, 且
上的单调奇函数, 且![]() .
.
(Ⅰ)求证函数![]() 为
为![]() 上的单调减函数;
上的单调减函数;
(Ⅱ) 解不等式![]() .
.
(Ⅰ)证明见解析
(Ⅱ)原不等式的解集为![]()
解析:
(Ⅰ)证明:∵函数![]() 是奇函数 ∴
是奇函数 ∴![]()
∵![]()
![]() ∴函数
∴函数![]() 不是
不是![]() 上的增函数--------------------------------2分
上的增函数--------------------------------2分
又函数![]() 在
在![]() 上单调 ∴函数
上单调 ∴函数![]() 为
为![]() 上的单调减函数-------------------4分
上的单调减函数-------------------4分
(Ⅱ)由![]() 得
得![]() ----------6分
----------6分
由(Ⅰ)知函数![]() 为
为![]() 上的单调减函数 ∴
上的单调减函数 ∴![]() ----------------8分
----------------8分
即![]()
![]() ,--------------------------------10分
,--------------------------------10分
![]() ∴原不等式的解集为
∴原不等式的解集为![]() --------------------------12分
--------------------------12分

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若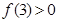 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;