题目内容
函数f(x)=
ax3+
ax2-2ax+2a+80的图象经过四个象限，则a的取值范围是
| 1 |
| 3 |
| 1 |
| 2 |
（-96，-15）
（-96，-15）
．分析：首先讨论a=0时原函数图象的情况，当a≠0时，求出原函数的导函数，分a＞0和a＜0两种情况讨论原函数的单调性，求出函数的极值点并求解极值，当a＞0时，要使原函数的图象经过四个象限，需要极大值大于0，且极小值小于0，此时a的值不存在；当a＜0时，要使原函数的图象经过四个象限，则需要极小值小于0，且极大值大于0，由此解得a的取值范围．
解答：解：由f(x)=
ax3+
ax2-2ax+2a+80，
若a=0时，原函数化为f（x）=80．为常数函数，不合题意；
f′（x）=ax2+ax-2a=a（x2+x-2）=a（x+2）（x-1）．
若a＞0时，当x∈（-∞，-2），x∈（1，+∞）时有f′（x）＞0，
函数f（x）在（-∞，-2），（1，+∞）上为增函数．
当x∈（-2，1）时，f′（x）＜0，函数f（x）在（-2，1）上为减函数．
所以函数f（x）在x=-2时取得极大值f(-2)=-
a+2a+4a+2a+80=80+
a．
函数f（x）在x=1时取得极小值f(1)=
a+
a-2a+2a+80=80+
a．
因为函数的图象先增后减再增，要使函数的图象经过四个象限，
则
，解①得：a＞-15．解②得：a＜-96．
此时a∈∅；
若a＜0，当x∈（-∞，-2），x∈（1，+∞）时有f′（x）＜0，
函数f（x）在（-∞，-2），（1，+∞）上为减函数．
当x∈（-2，1）时，f′（x）＞0，函数f（x）在（-2，1）上为增函数．
所以函数f（x）在x=-2时取得极小值f(-2)=-
a+2a+4a+2a+80=80+
a．
函数f（x）在x=1时取得极大值f(1)=
a+
a-2a+2a+80=80+
a．
为函数的图象先减后增再减，要使函数的图象经过四个象限，
则
，解得-96＜a＜-15．
所以使函数f(x)=
ax3+
ax2-2ax+2a+80的图象经过四个象限的a的取值范围是（-96，-15）．
故答案为（-96，-15）．
| 1 |
| 3 |
| 1 |
| 2 |
若a=0时，原函数化为f（x）=80．为常数函数，不合题意；
f′（x）=ax2+ax-2a=a（x2+x-2）=a（x+2）（x-1）．
若a＞0时，当x∈（-∞，-2），x∈（1，+∞）时有f′（x）＞0，
函数f（x）在（-∞，-2），（1，+∞）上为增函数．
当x∈（-2，1）时，f′（x）＜0，函数f（x）在（-2，1）上为减函数．
所以函数f（x）在x=-2时取得极大值f(-2)=-
| 8 |
| 3 |
| 16 |
| 3 |
函数f（x）在x=1时取得极小值f(1)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
因为函数的图象先增后减再增，要使函数的图象经过四个象限，
则
|
此时a∈∅；
若a＜0，当x∈（-∞，-2），x∈（1，+∞）时有f′（x）＜0，
函数f（x）在（-∞，-2），（1，+∞）上为减函数．
当x∈（-2，1）时，f′（x）＞0，函数f（x）在（-2，1）上为增函数．
所以函数f（x）在x=-2时取得极小值f(-2)=-
| 8 |
| 3 |
| 16 |
| 3 |
函数f（x）在x=1时取得极大值f(1)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
为函数的图象先减后增再减，要使函数的图象经过四个象限，
则
|
所以使函数f(x)=
| 1 |
| 3 |
| 1 |
| 2 |
故答案为（-96，-15）．
点评：本题考查了利用导数研究函数的极值，考查了函数的极值与函数图象之间的关系，思考该问题时考虑数与形的结合，属中档题．
练习册系列答案
名校课堂系列答案
相关题目
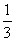(m∈R,e=2.718 28…是自然对数的底数).
.
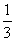(m∈R,e=2.718 28…是自然对数的底数).
.