题目内容
12．已知二项式（x5+$\frac{1}{x}$）n的展开式中含有常数项，则正整数n的最小值为6．分析 利用二项展开式的通项公式求出展开式的通项，令x的指数为0方程有解．由于n，r都是整数求出最小的正整数n即可．
解答 解：二项式（x5+$\frac{1}{x}$）n展开式的通项为：
Tr+1=Cnrx5n-6r，
令5n-6r=0，
据题意此方程有解，
∴n=$\frac{6}{5}$r，
当r=5时，n的最小值为6．
故答案为：6．
点评 本题考查了利用二项展开式的通项公式解决二项展开式的特定项问题，是基础题目．
练习册系列答案
相关题目
3．
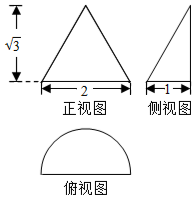已知某几何体的三视图如图所示，则该几何体的表面积为（ ）
已知某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | $\frac{5π}{2}+\sqrt{3}$ | B． | $\frac{3π}{2}+2$ | C． | $\frac{π}{2}+\sqrt{3}$ | D． | $\frac{3π}{2}+\sqrt{3}$ |
20．
某中学共有1000名学生参加考试，成绩如表：
（1）为了了解同学们的具体情况，学校将采取分层抽样的方法，抽取100名同学进行问卷调查，甲同学在本次测试中成绩为95分，求他被抽中的概率．
（2）本次数学成绩的优秀成绩为110分，试估计该中学达到优秀线的人数．
（3）作出频率分布直方图，并据此估计该校本次考试的平均分（用同一组中得到数据用该组区间的中点值作代表）
某中学共有1000名学生参加考试，成绩如表：| 成绩分组 | [0，30） | [30，60） | [60，90） | [90，120） | [120，150） |
| 人 数 | 60 | 90 | 300 | x | 160 |
（2）本次数学成绩的优秀成绩为110分，试估计该中学达到优秀线的人数．
（3）作出频率分布直方图，并据此估计该校本次考试的平均分（用同一组中得到数据用该组区间的中点值作代表）
17．现从男、女共8名学生干部中选出3名同学（要求3人中既有男同学又有女同学）分别参加全校“资源”、“生态”和“环保”三个夏令营活动，共有270种不同的安排，那么8名学生中男、女同学的人数分别是（ ）
| A． | 男同学1人，女同学7人 | B． | 男同学2人，女同学6人 | ||
| C． | 男同学3人，女同学5人 | D． | 男同学4人，女同学4人 |
4．已知$tan（α+\frac{π}{4}）=2$，则tan2α=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{5}$ | C． | $-\frac{3}{4}$ | D． | $-\frac{3}{5}$ |
2．已知等比数列{an}中，各项都是正数，且a1，$\frac{1}{2}$a3，2a2成等差数列，则$\frac{{a}_{6}+{a}_{7}}{{a}_{8}+{a}_{9}}$等于（ ）
| A． | 1+$\sqrt{2}$ | B． | 1-$\sqrt{2}$ | C． | 3+2$\sqrt{2}$ | D． | 3-2$\sqrt{2}$ |