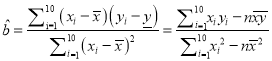题目内容
【题目】十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加.为了制定提升农民年收入、实现2020年脱贫的工作计划，该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图：
（1）根据频率分布直方图，估计50位农民的年平均收入
元（单位：千元）（同一组数据用该组数据区间的中点值表示）；
（2）由频率分布直方图，可以认为该贫困地区农民年收入X服从正态分布
，其中
近似为年平均收入，
近似为样本方差
，经计算得
，利用该正态分布，求：
（i）在扶贫攻坚工作中，若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入大约为多少千元？
（ii）为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1000位农民.若每位农民的年收入互相独立，问：这1000位农民中的年收入不少于12.14千元的人数最有可能是多少？
附参考数据：
，若随机变量X服从正态分布，则
，
，
.
【答案】（1）17.40千元；（2）（i）14.77千元.（ii）978人.
【解析】
（1）求解每一组数据的组中值与频率的乘积，将结果相加即可得到对应的
；
（2）（i）根据
的数值判断出年收入的取值范围，从而可计算出最低年收入；
（ii）根据
的数值判断出每个农民年收入不少于
千元的概率，然后根据二项分布的概率计算公式计算出“恰有
个农民年收入不少于”中的最大值即可.
解：（1）
千元
故估计50位农民的年平均收入为17.40千元；
（2）由题意知
（i）
，
所以
时，满足题意，
即最低年收入大约为14.77千元.
（ii）由
，
每个农民的年收入不少于12.14千元的事件的概率为0.9773，
记1000个农民的年收入不少于12.14千元的人数为
，
则
，其中
，
于是恰好有k个农民的年收入不少于12.14千元的事件概率为
，
从而由
得
，而
，
所以，当
时，
，
当
时，
，
由此可知，在所走访的1000位农民中，年收入不少于12.14千元的人数最有可能是978人.
