题目内容
已知函数f(x)=x2-1,g(x)=a|x-1|.
(1)当a=1时,解关于x的方程|f(x)|=g(x);
(2)当x∈R时,不等式f(x)≥g(x)恒成立,求实数a的取值范围;
(3)当实数a≥0时,求函数h(x)=|f(x)|+g(x)在区间[-2,2]上的最大值.
(1)当a=1时,解关于x的方程|f(x)|=g(x);
(2)当x∈R时,不等式f(x)≥g(x)恒成立,求实数a的取值范围;
(3)当实数a≥0时,求函数h(x)=|f(x)|+g(x)在区间[-2,2]上的最大值.
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)a=1时,方程|f(x)|=g(x);即:|x2-1|=|x-1|,讨论①显然,x=1是方程的解,②x≠1时,方程可化为|x+1|=1,解出即可,
(2)由(x2-1)≥a|x-1|(*)对x∈R恒成立,得①x=1时,(*)显然成立,此时a∈R,②x≠1时,(*)可化为a≤
,令φ(x)=
=
,解出即可,
(3)由h(x)=
,讨论①
>1,②0≤
≤1,即0≤a≤2时的情况,综合得出结论.
(2)由(x2-1)≥a|x-1|(*)对x∈R恒成立,得①x=1时,(*)显然成立,此时a∈R,②x≠1时,(*)可化为a≤
| x2-1 |
| |x-1| |
| x2-1 |
| |x-1| |
|
(3)由h(x)=
|
| a |
| 2 |
| a |
| 2 |
解答:
解:(1)a=1时,方程|f(x)|=g(x);
即:|x2-1|=|x-1|,
①显然,x=1是方程的解,
②x≠1时,方程可化为|x+1|=1,
解得:x=0,x=-2,
综上:原方程的解为{x|x=1,x=0,x=-2};
(2)不等式f(x)≥g(x)对x∈R恒成立,
即(x2-1)≥a|x-1|(*)对x∈R恒成立,
①x=1时,(*)显然成立,此时a∈R,
②x≠1时,(*)可化为a≤
,
令φ(x)=
=
,
当x>1时,φ(x)>2,当x<1时,φ(x)>-2,
故此时a≤-2,
综上:a≤-2.
(3)∵h(x)=|f(x)|+g(x)
=|x2-1|+a|x-1|
=
,
①
>1,即a>2时,h(x)在[-2,1]上递减,在[1,2]递增,
且h(-2)=3a+3,h(2)=a+3,
∴h(x)在[-2,2]上的最大值为3a+3,
②0≤
≤1,即0≤a≤2时,
h(x)在[-2,-1],[-
,1]递减,在[-1,-
],[1,2]递增,
且h(-2)=3a+3,h(2)=a+3,h(-
)=
+a+1,
∴h(x)在[-2,2]上的最大值为3a+3,
综上:当a≥0时,h(x)在[-2,2]上的最大值为3a+3.
即:|x2-1|=|x-1|,
①显然,x=1是方程的解,
②x≠1时,方程可化为|x+1|=1,
解得:x=0,x=-2,
综上:原方程的解为{x|x=1,x=0,x=-2};
(2)不等式f(x)≥g(x)对x∈R恒成立,
即(x2-1)≥a|x-1|(*)对x∈R恒成立,
①x=1时,(*)显然成立,此时a∈R,
②x≠1时,(*)可化为a≤
| x2-1 |
| |x-1| |
令φ(x)=
| x2-1 |
| |x-1| |
|
当x>1时,φ(x)>2,当x<1时,φ(x)>-2,
故此时a≤-2,
综上:a≤-2.
(3)∵h(x)=|f(x)|+g(x)
=|x2-1|+a|x-1|
=
|
①
| a |
| 2 |
且h(-2)=3a+3,h(2)=a+3,
∴h(x)在[-2,2]上的最大值为3a+3,
②0≤
| a |
| 2 |
h(x)在[-2,-1],[-
| a |
| 2 |
| a |
| 2 |
且h(-2)=3a+3,h(2)=a+3,h(-
| a |
| 2 |
| a2 |
| 4 |
∴h(x)在[-2,2]上的最大值为3a+3,
综上:当a≥0时,h(x)在[-2,2]上的最大值为3a+3.
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,分段函数问题,是一道综合题.

练习册系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)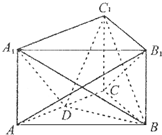 如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点. 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,CD⊥平面PAD,点O,E分别是AD,PC的中点,已知PA=PD,PO=AD=2BC=2CD=2.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,CD⊥平面PAD,点O,E分别是AD,PC的中点,已知PA=PD,PO=AD=2BC=2CD=2. AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1