题目内容
13.给出下列四种说法:①函数y=ax(a>0,且a≠1)与函数y=log1ax(a>0,且a≠1)的定义域相同;
②函数y=x3与y=3x的值域相同;
③函数y=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$与y=$\frac{(1+{2}^{x})^{2}}{x•{2}^{x}}$均是奇函数;
④函数y=(x-1)2与y=2x-1在(0,+∞)上都是增函数.
其中正确说法的序号是①③.
分析 ①,∵ax>0(a>0,且a≠1)∴函数y=log1ax(a>0,且a≠1)的定义域为R;
②,函数y=x3的值域为R,y=3x的值域为(0,+∞);
③,∵函数y=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$与y=$\frac{(1+{2}^{x})^{2}}{x•{2}^{x}}$的定义域均关于原点对称,且$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$$\frac{1}{2}+\frac{1}{{2}^{-x}-1}=0$,$\frac{(1+{2}^{-x})^{2}}{-x•{2}^{-x}}$+$\frac{(1+{2}^{x})^{2}}{x•{2}^{x}}$=0;
④,函数y=(x-1)2 (1,+∞)上都是增函数.
解答 解:对于①,∵ax>0(a>0,且a≠1)∴函数y=ax(a>0,且a≠1)与函数y=log1ax(a>0,且a≠1)的定义域相同,故正确;
对于②,函数y=x3的值域为R,y=3x的值域为(0,+∞),故错;
对于③,∵函数y=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$与y=$\frac{(1+{2}^{x})^{2}}{x•{2}^{x}}$的定义域均关于原点对称,且$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$$\frac{1}{2}+\frac{1}{{2}^{-x}-1}=0$,$\frac{(1+{2}^{-x})^{2}}{-x•{2}^{-x}}$+$\frac{(1+{2}^{x})^{2}}{x•{2}^{x}}$=0,故均是奇函数,故正确;
对于④,函数y=(x-1)2 (1,+∞)上都是增函数,故错.
故答案:①③.
点评 本题考查了命题真假的判定,涉及到了函数的概念及性质,属于基础题.

| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
| A. | 若a⊥α,b∥β,a⊥b,则α⊥β | B. | 若a⊥α,b∥β,a∥b,则α∥β | ||
| C. | 若a⊥α,a∥β,则α⊥β | D. | 若a∥β,b∥β,则α∥b |
| A. | (-1,0] | B. | [-1,0] | C. | [0,1) | D. | [0,1] |
| A. | $\sqrt{2}$f(-$\frac{π}{3}$)<f($\frac{π}{4}$) | B. | $\sqrt{2}$f(-$\frac{π}{3}$)<f(-$\frac{π}{4}$) | C. | f(0)$>\sqrt{2}$f(-$\frac{π}{4}$) | D. | f($\frac{π}{4}$)$<\sqrt{3}$f($\frac{π}{3}$) |
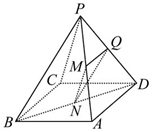 如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,
如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,