题目内容
已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上最大值为20,求它在该区间上的最小值。

(2)因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,所以f(x)在[-1,2]因为在(-1,3)上f’(x)>0,所以f(x)在[-1,2]上单调递增,又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是22+a=20,解得a=-2.
故f(x)=-x3+3x2+9x-2,因此,f{-1}=1+3-9-2=-7
即函数f(x)在区间[-2,2]上的最小值为-7。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 z满足
z满足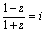 ,则|1
,则|1 +z|= ( )
+z|= ( )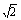 D.2
D.2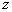 满足方程
满足方程 ,则
,则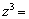
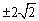 B.
B.  C.
C. 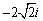 D.
D. 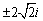

 (D)2- i
(D)2- i 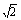 cosx的图像,只需将函数y=
cosx的图像,只需将函数y= )的图像上所有的点的 ( )
)的图像上所有的点的 ( )  横坐标缩短到原来的
横坐标缩短到原来的 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 个单位长度
个单位长度  数f(x)=logax(a>0且a≠1),若数列:2,f(a1),f(2),…,f(an),2n+4(n∈N*)成等差数列。
数f(x)=logax(a>0且a≠1),若数列:2,f(a1),f(2),…,f(an),2n+4(n∈N*)成等差数列。 Sn;
Sn;