ΧβΡΩΡΎ»ί
Ε®“εœρΝΩ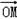 =Θ®aΘ§bΘ©ΒΡΓΑœύΑιΚ· ΐΓ±ΈΣfΘ®xΘ©=asinx+bcosxΘ§Κ· ΐfΘ®xΘ©=asinx+bcosxΒΡΓΑœύΑιœρΝΩΓ±ΈΣ
=Θ®aΘ§bΘ©ΒΡΓΑœύΑιΚ· ΐΓ±ΈΣfΘ®xΘ©=asinx+bcosxΘ§Κ· ΐfΘ®xΘ©=asinx+bcosxΒΡΓΑœύΑιœρΝΩΓ±ΈΣ =Θ®aΘ§bΘ©Θ®Τδ÷–OΈΣΉχ±ξ‘≠ΒψΘ©Θ§Φ«ΤΫΟφΡΎΥυ”–œρΝΩΒΡΓΑœύΑιΚ· ΐΓ±ΙΙ≥…ΒΡΦ·ΚœΈΣSΓΘ
=Θ®aΘ§bΘ©Θ®Τδ÷–OΈΣΉχ±ξ‘≠ΒψΘ©Θ§Φ«ΤΫΟφΡΎΥυ”–œρΝΩΒΡΓΑœύΑιΚ· ΐΓ±ΙΙ≥…ΒΡΦ·ΚœΈΣSΓΘ
Θ®1Θ©…ηgΘ®xΘ©=3sinΘ®x+ Θ©+4sinxΘ§«σ÷ΛΘΚgΘ®xΘ©Γ SΘΜ
Θ©+4sinxΘ§«σ÷ΛΘΚgΘ®xΘ©Γ SΘΜ
Θ®2Θ©“―÷ΣhΘ®xΘ©=cosΘ®x+ΠΝΘ©+2cosxΘ§«“hΘ®xΘ©Γ SΘ§«σΤδΓΑœύΑιœρΝΩΓ±ΒΡΡΘΘΜ
Θ®3Θ©“―÷ΣMΘ®aΘ§bΘ©Θ®bΓΌ0Θ©ΈΣ‘≤CΘΚΘ®x-2Θ©2+y2=1…œ“ΜΒψΘ§œρΝΩ ΒΡΓΑœύΑιΚ· ΐΓ±fΘ®xΘ©‘Ύx=x0¥Π»ΓΒΟΉν¥σ÷ΒΘ§Β±ΒψM‘Ύ‘≤C…œ‘ΥΕ· ±Θ§«σtan2x0ΒΡ»Γ÷ΒΖΕΈßΓΘ
ΒΡΓΑœύΑιΚ· ΐΓ±fΘ®xΘ©‘Ύx=x0¥Π»ΓΒΟΉν¥σ÷ΒΘ§Β±ΒψM‘Ύ‘≤C…œ‘ΥΕ· ±Θ§«σtan2x0ΒΡ»Γ÷ΒΖΕΈßΓΘ
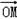 =Θ®aΘ§bΘ©ΒΡΓΑœύΑιΚ· ΐΓ±ΈΣfΘ®xΘ©=asinx+bcosxΘ§Κ· ΐfΘ®xΘ©=asinx+bcosxΒΡΓΑœύΑιœρΝΩΓ±ΈΣ
=Θ®aΘ§bΘ©ΒΡΓΑœύΑιΚ· ΐΓ±ΈΣfΘ®xΘ©=asinx+bcosxΘ§Κ· ΐfΘ®xΘ©=asinx+bcosxΒΡΓΑœύΑιœρΝΩΓ±ΈΣ =Θ®aΘ§bΘ©Θ®Τδ÷–OΈΣΉχ±ξ‘≠ΒψΘ©Θ§Φ«ΤΫΟφΡΎΥυ”–œρΝΩΒΡΓΑœύΑιΚ· ΐΓ±ΙΙ≥…ΒΡΦ·ΚœΈΣSΓΘ
=Θ®aΘ§bΘ©Θ®Τδ÷–OΈΣΉχ±ξ‘≠ΒψΘ©Θ§Φ«ΤΫΟφΡΎΥυ”–œρΝΩΒΡΓΑœύΑιΚ· ΐΓ±ΙΙ≥…ΒΡΦ·ΚœΈΣSΓΘΘ®1Θ©…ηgΘ®xΘ©=3sinΘ®x+
 Θ©+4sinxΘ§«σ÷ΛΘΚgΘ®xΘ©Γ SΘΜ
Θ©+4sinxΘ§«σ÷ΛΘΚgΘ®xΘ©Γ SΘΜΘ®2Θ©“―÷ΣhΘ®xΘ©=cosΘ®x+ΠΝΘ©+2cosxΘ§«“hΘ®xΘ©Γ SΘ§«σΤδΓΑœύΑιœρΝΩΓ±ΒΡΡΘΘΜ
Θ®3Θ©“―÷ΣMΘ®aΘ§bΘ©Θ®bΓΌ0Θ©ΈΣ‘≤CΘΚΘ®x-2Θ©2+y2=1…œ“ΜΒψΘ§œρΝΩ
 ΒΡΓΑœύΑιΚ· ΐΓ±fΘ®xΘ©‘Ύx=x0¥Π»ΓΒΟΉν¥σ÷ΒΘ§Β±ΒψM‘Ύ‘≤C…œ‘ΥΕ· ±Θ§«σtan2x0ΒΡ»Γ÷ΒΖΕΈßΓΘ
ΒΡΓΑœύΑιΚ· ΐΓ±fΘ®xΘ©‘Ύx=x0¥Π»ΓΒΟΉν¥σ÷ΒΘ§Β±ΒψM‘Ύ‘≤C…œ‘ΥΕ· ±Θ§«σtan2x0ΒΡ»Γ÷ΒΖΕΈßΓΘΫβΘΚΘ®1Θ©gΘ®xΘ©=3sinΘ®x+  Θ©+4sinx=4sinx+3cosxΘ§
ȩ+4sinx=4sinx+3cosxȧ
ΤδΓ°œύΑιœρΝΩΓ· =Θ®4Θ§3Θ©Θ§gΘ®xΘ©Γ SΓΘ
=Θ®4Θ§3Θ©Θ§gΘ®xΘ©Γ SΓΘ
Θ®2Θ©hΘ®xΘ©=cosΘ®x+ΠΝΘ©+2cosx =Θ®cosxcosΠΝ-sinxsinΠΝΘ©+2cosx =-sinΠΝsinx+Θ®cosΠΝ+2Θ©cosx
ΓύΚ· ΐhΘ®xΘ©ΒΡΓ°œύΑιœρΝΩΓ· =Θ®-sinΠΝΘ§cosΠΝ+2Θ©
=Θ®-sinΠΝΘ§cosΠΝ+2Θ©
‘ρ| |=
|=  =
= ΓΘ
ΓΘ
Θ®3Θ© ΒΡΓ°œύΑιΚ· ΐΓ·fΘ®xΘ©=asinx+bcosx=
ΒΡΓ°œύΑιΚ· ΐΓ·fΘ®xΘ©=asinx+bcosx= sinΘ®x+Π’Θ©Θ§
sinΘ®x+Π’Θ©Θ§
Τδ÷–cosΠ’= Θ§sinΠ’=
Θ§sinΠ’= Θ°
Θ°
Β±x+Π’=2kΠ–+ Θ§kΓ Z ±Θ§fΘ®xΘ©»ΓΒΫΉν¥σ÷ΒΘ§Ι x0=2kΠ–+
Θ§kΓ Z ±Θ§fΘ®xΘ©»ΓΒΫΉν¥σ÷ΒΘ§Ι x0=2kΠ–+ -Π’Θ§kΓ Z
-Π’Θ§kΓ Z
Γύtanx0=tanΘ®2kΠ–+ -Π’Θ©=cotΠ’=
-Π’Θ©=cotΠ’= Θ§tan2x0=
Θ§tan2x0= =
= =
=
 ΈΣ÷±œΏOMΒΡ–±¬ Θ§”…ΦΗΚΈ“β“ε÷ΣΘΚ
ΈΣ÷±œΏOMΒΡ–±¬ Θ§”…ΦΗΚΈ“β“ε÷ΣΘΚ Γ [-
Γ [- Θ§0Θ©Γ»Θ®0Θ§
Θ§0Θ©Γ»Θ®0Θ§ ]
]
Ννm= Θ§‘ρtan2x0=
Θ§‘ρtan2x0= Θ§mΓ [-
Θ§mΓ [- Θ§0Θ©Γ»Θ®0Θ§
Θ§0Θ©Γ»Θ®0Θ§ }
}
Β±- ΓήmΘΦ0 ±Θ§Κ· ΐtan2x0=
ΓήmΘΦ0 ±Θ§Κ· ΐtan2x0= ΒΞΒςΒίΦθΘ§
ΒΞΒςΒίΦθΘ§
Γύ0ΘΦtan2x0Γή ΘΜ
ΘΜ
Β±0ΘΦmΓή ±Θ§Κ· ΐtan2x0=
±Θ§Κ· ΐtan2x0= ΒΞΒςΒίΦθΘ§
ΒΞΒςΒίΦθΘ§
Γύ- Γήtan2x0ΘΦ0
Γήtan2x0ΘΦ0
Ήέ…œΥυ ωΘ§tan2x0Γ [- Θ§0Θ©Γ»Θ®0Θ§
Θ§0Θ©Γ»Θ®0Θ§ ]ΓΘ
]ΓΘ
 ȩ+4sinx=4sinx+3cosxȧ
Θ©+4sinx=4sinx+3cosxΘ§ΤδΓ°œύΑιœρΝΩΓ·
 =Θ®4Θ§3Θ©Θ§gΘ®xΘ©Γ SΓΘ
=Θ®4Θ§3Θ©Θ§gΘ®xΘ©Γ SΓΘΘ®2Θ©hΘ®xΘ©=cosΘ®x+ΠΝΘ©+2cosx =Θ®cosxcosΠΝ-sinxsinΠΝΘ©+2cosx =-sinΠΝsinx+Θ®cosΠΝ+2Θ©cosx
ΓύΚ· ΐhΘ®xΘ©ΒΡΓ°œύΑιœρΝΩΓ·
 =Θ®-sinΠΝΘ§cosΠΝ+2Θ©
=Θ®-sinΠΝΘ§cosΠΝ+2Θ©‘ρ|
 |=
|=  =
= ΓΘ
ΓΘΘ®3Θ©
 ΒΡΓ°œύΑιΚ· ΐΓ·fΘ®xΘ©=asinx+bcosx=
ΒΡΓ°œύΑιΚ· ΐΓ·fΘ®xΘ©=asinx+bcosx= sinΘ®x+Π’Θ©Θ§
sinΘ®x+Π’Θ©Θ§Τδ÷–cosΠ’=
 Θ§sinΠ’=
Θ§sinΠ’= Θ°
Θ°Β±x+Π’=2kΠ–+
 Θ§kΓ Z ±Θ§fΘ®xΘ©»ΓΒΫΉν¥σ÷ΒΘ§Ι x0=2kΠ–+
Θ§kΓ Z ±Θ§fΘ®xΘ©»ΓΒΫΉν¥σ÷ΒΘ§Ι x0=2kΠ–+ -Π’Θ§kΓ Z
-Π’Θ§kΓ ZΓύtanx0=tanΘ®2kΠ–+
 -Π’Θ©=cotΠ’=
-Π’Θ©=cotΠ’= Θ§tan2x0=
Θ§tan2x0= =
= =
=
 ΈΣ÷±œΏOMΒΡ–±¬ Θ§”…ΦΗΚΈ“β“ε÷ΣΘΚ
ΈΣ÷±œΏOMΒΡ–±¬ Θ§”…ΦΗΚΈ“β“ε÷ΣΘΚ Γ [-
Γ [- Θ§0Θ©Γ»Θ®0Θ§
Θ§0Θ©Γ»Θ®0Θ§ ]
]Ννm=
 Θ§‘ρtan2x0=
Θ§‘ρtan2x0= Θ§mΓ [-
Θ§mΓ [- Θ§0Θ©Γ»Θ®0Θ§
Θ§0Θ©Γ»Θ®0Θ§ }
}Β±-
 ΓήmΘΦ0 ±Θ§Κ· ΐtan2x0=
ΓήmΘΦ0 ±Θ§Κ· ΐtan2x0= ΒΞΒςΒίΦθΘ§
ΒΞΒςΒίΦθΘ§Γύ0ΘΦtan2x0Γή
 ΘΜ
ΘΜΒ±0ΘΦmΓή
 ±Θ§Κ· ΐtan2x0=
±Θ§Κ· ΐtan2x0= ΒΞΒςΒίΦθΘ§
ΒΞΒςΒίΦθΘ§Γύ-
 Γήtan2x0ΘΦ0
Γήtan2x0ΘΦ0Ήέ…œΥυ ωΘ§tan2x0Γ [-
 Θ§0Θ©Γ»Θ®0Θ§
Θ§0Θ©Γ»Θ®0Θ§ ]ΓΘ
]ΓΘ
ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ