题目内容
 是定义在R上的增函数,则下列结论一定正确的是( )
是定义在R上的增函数,则下列结论一定正确的是( )A. 是偶函数且是增函数 是偶函数且是增函数 | B. 是偶函数且是减函数 是偶函数且是减函数 |
C. 是奇函数且是增函数 是奇函数且是增函数 | D.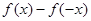 是奇函数且是减函数 是奇函数且是减函数 |
C
本题考查函数的奇偶性和单调性的概念.
A错误.设 是增函数,但
是增函数,但 是常数函数;同理B错误;
是常数函数;同理B错误;
C正确.设 则
则 ;函数
;函数 是奇函数;任取
是奇函数;任取

 因为
因为 是是定义在R上的增函数,所以
是是定义在R上的增函数,所以 ;所以
;所以
 ,即
,即  所以函数
所以函数 是增函数;D错误.故选C
是增函数;D错误.故选C
A错误.设
 是增函数,但
是增函数,但 是常数函数;同理B错误;
是常数函数;同理B错误;C正确.设
 则
则 ;函数
;函数 是奇函数;任取
是奇函数;任取

 因为
因为 是是定义在R上的增函数,所以
是是定义在R上的增函数,所以 ;所以
;所以 ,即
,即  所以函数
所以函数 是增函数;D错误.故选C
是增函数;D错误.故选C
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为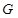 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 , 深为3 m。如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?
, 深为3 m。如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?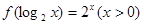 ,则
,则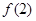 的值是( )
的值是( )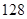
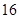
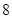
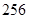
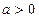 ,函数
,函数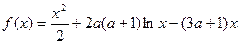 .
.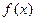 在
在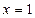 处的切线与直线
处的切线与直线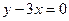 平行,求
平行,求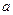 的值;
的值;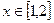 ,
,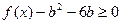 恒成立,求实数
恒成立,求实数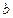 的取值组成的集合.
的取值组成的集合.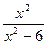 ,
, 定义域;
定义域;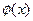 ] = lgx,求
] = lgx,求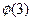 的值。
的值。 的单调递增区间是
的单调递增区间是 的所有实根之和等于_______________
的所有实根之和等于_______________