题目内容
已知椭圆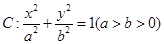 的一个焦点是
的一个焦点是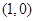 ,两个焦点与短轴的一个端点构成等边三角形.
,两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点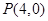 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线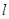 交椭圆
交椭圆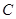 于
于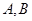 两点,设点
两点,设点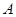 关于
关于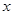 轴
轴
的对称点为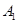 .
.
(i)求证:直线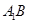 过
过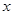 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ii)求△ 面积的取值范围。
面积的取值范围。
【答案】
(2) ;(2)
;(2) ,
, .
.
【解析】本试题主要是考查了椭圆的方程的求解以及直线与坐标轴的交点问题和三角形面积的计算。
解:(Ⅰ)易得 ,则
,则 所以椭圆的标准方程为
所以椭圆的标准方程为
(Ⅱ)(i)不妨设直线方程为 ,代入
,代入
得: ,
,
设 ,则有
,则有 ,
, ,
,
由 关于
关于 轴的对称点为
轴的对称点为 ,得
,得 ,
,
根据题设条件设定点为 ,
,
得 ,即
,即 ,整理得
,整理得 ,
,
 ,代入得
,代入得
则定点为
(ii)由(I)中判别式 ,解得
,解得 ,而直线
,而直线 过定点
过定点
所以
记 ,
, ,易得
,易得 在
在 上位单调递减函数,
上位单调递减函数,
得 

练习册系列答案
相关题目
(本小题满分12分)
|
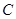 :
: 的一个焦点是(1,0),两个焦点与短轴的一个端点
的一个焦点是(1,0),两个焦点与短轴的一个端点
构成等边三角形.
(Ⅰ)求椭圆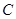 的方程;
的方程;
(Ⅱ)过点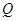 (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线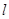 交椭圆
交椭圆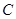 于
于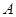 、
、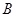 两点,设点
两点,设点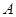 关于
关于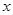 轴的对称点为
轴的对称点为 .
.
(ⅰ)求证:直线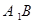 过
过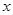 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ⅱ)求△ 面积的取值范围.
面积的取值范围.
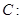
 的一个焦点是
的一个焦点是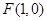 ,且离心率为
,且离心率为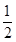 .
.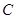 的方程;
的方程;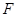 的直线交椭圆
的直线交椭圆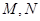 两点,线段
两点,线段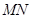 的垂直平分线交
的垂直平分线交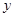 轴于点
轴于点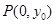 ,求
,求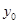 的取值范围.
的取值范围.