Question

焦点为（0，4）和（0，-4），且过点的椭圆方程是________．

Answer 1

分析：先由条件求出半焦距和焦点所在的坐标轴，待定系数法设出椭圆的方程，把椭圆经过的点的坐标代入椭圆的方程，即可求出待定系数，从而得到椭圆的标准方程．
解答：由题意知，c=4，焦点在 y轴上，
∴a²=b²+16，故可设椭圆的方程为 ，
把点代入椭圆的方程可求得 b²=20，
故椭圆的方程为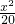+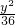=1，
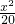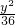故答案为：+=1．
点评：本题考查用待定系数法求椭圆的标准方程，以及椭圆方程中a、b、c之间的关系．属于基础题．