题目内容
(1)计算cos300°-sin(-330°)+tan675°
(2)化简
(n∈Z).
(2)化简
| sin[α+(2n+1)π]+sin[α-(2n+1)π] | sin(α+2nπ)•cos(α-2nπ) |
分析:(1)原式各项中的角度变形后,利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果;
(2)原式利用诱导公式化简,约分即可得到结果.
(2)原式利用诱导公式化简,约分即可得到结果.
解答:解:(1)原式=cos(360°-60°)+sin(360°-30°)+tan(720°-45°)=cos60°-sin30°-tan45°=
-
-1=-1;
(2)原式=
=
=-
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)原式=
| -sinα-sinα |
| sinαcosα |
| -2sinα |
| sinαcosα |
| 2 |
| cosα |
点评:此题考查了诱导公式的作用,以及特殊角的三角函数值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
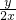 ,①是正数;②是负数;③等于零;④没有意义?
,①是正数;②是负数;③等于零;④没有意义?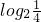
 ;②
;② .
. .
. .
. ,①是正数;②是负数;③等于零;④没有意义?
,①是正数;②是负数;③等于零;④没有意义?
 ;②
;② .
. .
. .
.