题目内容
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上是减函数,求
上是减函数,求![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() ,若函数
,若函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意结合函数单调性的定义得到关于a的表达式,结合指数函数的性质确定![]() 的取值范围即可;
的取值范围即可;
(2)利用换元法将原问题转化为二次方程根的分布问题,然后求解实数![]() 的取值范围即可.
的取值范围即可.
(1)由题设,若![]() 在
在![]() 上是减函数,
上是减函数,
则任取![]() ,
,![]() ,且
,且![]() ,都有
,都有![]() ,即
,即![]() 成立.
成立.
∵![]()
![]()
![]()
![]()
![]() .
.
又![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,
∴由![]() ,得
,得![]() ,
,
即![]() ,且
,且![]() .
.
∴只须![]() ,解
,解![]() .
.
由![]() ,
,![]() ,且
,且![]() ,知
,知![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
所以![]() 在
在![]() 上是减函数,实数
上是减函数,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由题知方程![]() 有且只有一个实数根,
有且只有一个实数根,
令![]() ,则关于
,则关于![]() 的方程
的方程![]() 有且只有一个正根.
有且只有一个正根.
若![]() ,则
,则![]() ,不符合题意,舍去;
,不符合题意,舍去;
若![]() ,则方程
,则方程![]() 两根异号或有两个相等的正根.
两根异号或有两个相等的正根.
方程![]() 两根异号等价于
两根异号等价于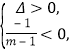 解得
解得![]() ;
;
方程![]() 有两个相等的正根等价于
有两个相等的正根等价于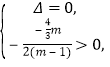 解得
解得![]() ;
;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于0的常数),现随机抽取6件合格产品,测得数据如下:
为大于0的常数),现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
(1)求![]() 关于
关于![]() 的回归方程;(提示:
的回归方程;(提示:![]() 与
与![]() 有线性相关关系)
有线性相关关系)
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
参考数据及公式:
![]() ,
,![]() ,
,![]() ,
,![]()
对于样本![]() (
(![]() ),其回归直线
),其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
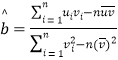 ,
,![]()
