题目内容
直线l1:(m+2)x+(m2-3m)y+4=0,l2:2x+4(m-3)y-1=0,如果l1∥l2,则m的值为( )
| A、-4 | B、0 | C、3 | D、-4或3 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(1)当l1,l2斜率都存在时,由平行可得-
=-
,解得m验证可得;(2)当l1,l2斜率不存在时
解得m=3,代入验证即可.
| m+2 |
| m2-3m |
| 2 |
| 4(m-3) |
|
解答:
解:(1)当l1,l2斜率都存在时
,∴m≠0且m≠3.
由l1∥l2得-
=-
,解得m=-4.
此时l1:x-14y-2=0,l2:x-14y-
=0,
显然,l1与l2不重合,满足条件.
(2)当l1,l2斜率不存在时
解得m=3.
此时l1:x=-
,l2:x=
,满足条件.
综上所述,m=-4或m=3.
故选:D
|
由l1∥l2得-
| m+2 |
| m2-3m |
| 2 |
| 4(m-3) |
此时l1:x-14y-2=0,l2:x-14y-
| 1 |
| 2 |
显然,l1与l2不重合,满足条件.
(2)当l1,l2斜率不存在时
|
此时l1:x=-
| 4 |
| 5 |
| 1 |
| 2 |
综上所述,m=-4或m=3.
故选:D
点评:本题考查直线的一般式方程与平行关系,涉及分类讨论的思想,属基础题.

练习册系列答案
相关题目
下面四个命题正确的是( )
| A、10以内的质数集合是{0,2,3,5,7} |
| B、由1,2,3组成的集合可表示为{1,2,3}或{3,1,2} |
| C、方程x2-2x+1=0的解集是{1,1} |
| D、0与{0}表示同一个集合 |
如图(1)、(2)、(3)、(4)是四个几何体的三视图,这四个几何体依次分别是( )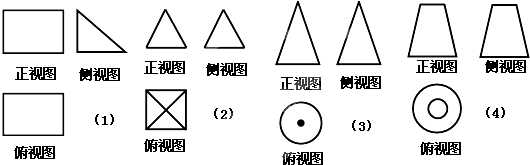

| A、三棱台、三棱柱、圆锥、圆台 |
| B、三棱台、三棱锥、圆锥、圆台 |
| C、三棱柱、四棱锥、圆锥、圆台 |
| D、三棱柱、三棱台、圆锥、圆台 |
若直线l1:(a-1)x+4y-3=0与l2:(a-2)x-5y+a-3=0互相垂直,则实数a的值为( )
| A、-3或6 | B、3或-6 |
| C、-3 | D、3或6 |
已知cos(
+θ)=
,则sin(
π-θ)的值为( )
| π |
| 6 |
| 1 |
| 2 |
| 4 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|